the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Laboratory and numerical experiments on stem waves due to monochromatic waves along a vertical wall
Sung Bum Yoon
Jong-In Lee
Young-Take Kim
Choong Hun Shin
In this study, both laboratory and numerical experiments are conducted to investigate stem waves propagating along a vertical wall developed by the incidence of monochromatic waves. The results show the following features: for small-amplitude waves, the wave heights along the wall show a slowly varying undulation. Normalized wave heights perpendicular to the wall show a standing wave pattern. The overall wave pattern in the case of small-amplitude waves shows a typical diffraction pattern around a semi-infinite thin breakwater. As the amplitude of incident waves increases, both the undulation intensity and the asymptotic normalized wave height decrease along the wall. For larger-amplitude waves with smaller angle of incidence, the measured data clearly show stem waves. Numerical simulation results are in good agreement with the results of laboratory experiments. The results of present experiments favorably support the existence and the properties of stem waves found by other researchers using numerical simulations. The characteristics of the stem waves generated by the incidence of monochromatic Stokes waves are compared with those of the Mach stem of solitary waves.
- Article
(5549 KB) -
Supplement
(2598 KB) - BibTeX
- EndNote
Coastal structures have been increasingly constructed in deep water regions as the size of ships becomes larger. In such deep water regions, a vertical-type structure is preferred to save construction costs. In the case of a vertical structure, stem waves occur when waves propagate obliquely against the structure. Thus, there is a need for careful consideration to secure appropriate free board and stability of caisson blocks.
Based on laboratory experiments of the reflection of a solitary wave propagating obliquely against a vertical wall, Perroud (1957) reported the existence of three types of waves when the angle between incident wave ray and a vertical wall is below 45∘: incident, reflected, and stem waves. On the one hand, Berger and Kohlhase (1976) conducted laboratory experiments and found that stem waves appeared also in the case of sinusoidal waves, and that the properties of stem waves developed by sinusoidal waves showed similarities to those of solitary waves. On the other hand, according to laboratory experiments by Melville (1980) with solitary waves, the width and height of stem waves were found to be wider and larger, respectively, as waves propagated along the wall. However, the wave height did not exceed double the height of incident waves. Yue and Mei (1980) analyzed stem waves at a constant water depth using parabolic approximation equations for second-order Stokes waves. They found that the influence of reflected waves vanished when the incident angle between the structure and the waves was below 20∘ and that only incident waves and stem waves appeared. Liu and Yoon (1986) showed that stem waves occurred also in an area along the line of a depth discontinuity, as in the case of a vertical wall. In addition, Yoon and Liu (1989) introduced a parabolic approximation equation based on the Boussinesq equation and analyzed stem waves for the case of cnoidal incident waves. Yoon and Liu (1989) showed the importance of the incident wave nonlinearity. Most previous studies on stem waves focused on the properties of stem waves depending on the incident angle and wave nonlinearity of monochromatic waves.
While the stem waves generated by the sinusoidal waves have drawn less attention in recent years, the Mach stem induced by the interaction between the line solitons in the shallow-waters has continuously attracted the attention of the researchers. Since the pioneering work of Miles (1977a, b) on the obliquely interacting solitary waves, the soliton interactions have been extensively studied. Miles (1977b) developed an analytical solution to predict the amplification of the stem wave along the wall as a function of the interaction parameter, , where H0, h, and θ0 are the wave height, the water depth, and the incident angle of solitary wave, respectively. When , the amplification of a solitary wave can reach 4 times that of the incident wave. Soomere (2004) investigated the soliton interactions based on the KP equation (Kadomtsev and Petviashvili, 1970). Kodama et al. (2009) and Kodama (2010) proposed the modified interaction parameter, ). Li et al. (2011) conducted a precision laboratory experiment to capture the detailed features of Mach reflection using the LIF (laser-induced fluorescent) technique. The laboratory data of Li et al. (2011) strongly support the theory of Miles (1977b) except the cases where the κ∗ value lies in the neighborhood of the 4-fold amplification. Funakoshi (1980), Tanaka (1993), Li et al. (2011), and Gidel et al. (2017) performed numerical experiments to verify the Miles' 4-fold amplification. As summarized by Li et al. (2011) and Gidel et al. (2017) most of the models underestimated the 4-fold amplification due to the limitations of the computational resources. The amplification ratio of 3.6 obtained by Gidel et al. (2017) is so far the maximum among the numerical results showing the full development stage of stem waves.
Even though the existence and the properties of stem waves for sinusoidal waves are well known theoretically via numerical simulations (e.g., Yue and Mei, 1980; Yoon and Liu, 1989), they are not yet fully supported by physical experiments. Berger and Kohlhase (1976) conducted hydraulic experiments to show the existence of stem waves for the cases of sinusoidal waves. Their experimental data, however, failed to produce clear stem waves, possibly due to partial reflection from the beach, diffraction from the ends of vertical wall, or insufficient space in the wave basin. Lee et al. (2003), Lee and Yoon (2006) and Lee and Kim (2007) performed laboratory experiments to investigate stem waves for sinusoidal waves and compared the measured waves with the numerical results obtained using a nonlinear parabolic approximation equation model. Their hydraulic experiments demonstrated stem waves for some cases with a relatively large incident wave. However, the stem waves were not clearly developed because of both the narrowness of the wave basin and the reflected waves from the beach. Only four cases of incident wave conditions were tested in their experiment. Thus, the experimental data were not sufficient to investigate the properties of stem waves. Moreover, the numerical results for the cases of large angle of incidence were not highly accurate because of the small-angle parabolic model employed for their numerical simulations. Thus, there is still need to perform a precisely controlled experiment to investigate the existence and the properties of stem waves.
In this study, precisely controlled laboratory experiments are conducted to investigate the characteristics of stem waves developed by the incidence of monochromatic waves. The measured data are compared with numerical simulations and analytical solutions. In the following section, the numerical simulation method and the analytical solution employed in this study are summarized. In Sect. 3, the experimental setup and procedure are briefly presented. In Sect. 4, the measured wave heights are compared with numerically simulated results and analytical solutions. In Sect. 5, the characteristics of the stem waves generated by the incidence of monochromatic Stokes waves are compared with those of the Mach stem of solitary waves. In the final section, the major findings from this study are summarized.
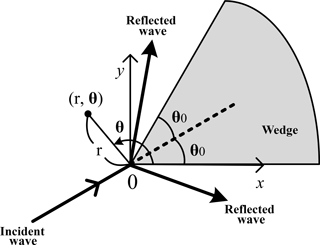
In this study, the stem waves that have developed along a vertical wall over a constant water depth are investigated for the cases of monochromatic waves. Figure 1 shows a sketch of the wave field around a vertical wedge. The monochromatic waves are symmetrically incident towards the tip of the wedge. The x axis of the coordinate system is aligned with a side wall of the wedge. The angle of incidence θ0 is defined as the angle between the x axis and the incident wave ray. The computational domain lies in the region of 0 ≤ x and y ≤ 0.
2.1 Numerical simulation method
To compare with our experiments, the latest version of REF/DIF, a wide-angle nonlinear parabolic approximation equation model developed by Kirby et al. (2002), is employed to simulate stem waves. The REF/DIF model can deal with the refraction–diffraction of Stokes waves of third-order nonlinearity over a slowly varying depth and current. Due to the use of parabolic formulation the reflection in the main direction of propagation is forbidden, but not in the transverse direction. In this study, the water depth is uniform, and no ambient current is present. With no current and energy dissipation on a constant water depth and by selecting a (1, 1) Padé approximant in the model, the governing equation of the REF/DIF model is simplified as
where h is the water depth, , Cg is the wave group velocity, A is the complex wave amplitude, and k and ω are the wave number and the angular frequency, respectively, and satisfy the following linear dispersion relationship:
where g is the gravitational acceleration, and D is given as
The third term of Eq. (1) is the correction term obtained by selecting the (1, 1) Padé approximant for the wide-angle parabolic approximation. According to Fig. 2 of Kirby (1986) the accuracy of the waves propagating obliquely to the main direction of propagation, i.e., x direction, can be maintained up to ±45∘. In this study the range of the incidence angles of both incident and reflected waves lies from ±10 to ±40∘. Thus, the sufficient accuracy of the numerical solution is expected.
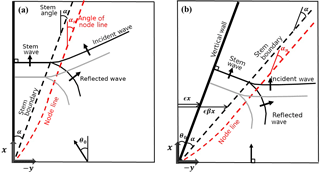
The conventional parabolic approximation equation, i.e., the nonlinear Schrödinger equation of Yue and Mei (1980), is obtained if this term is neglected. The last term in Eq. (1) describes the nonlinear self-interaction of waves. Figure 2 shows the coordinate system for the present numerical simulation in comparison with that of Yue and Mei (1980). In the present simulation the incident waves are prescribed obliquely along the y axis as
where a0 is the amplitude of the incident wave, and kn is the wave number with the nonlinear correction given as
where is the phase speed of wave. The no-flux boundary condition is prescribed along the vertical wall (y=0) given as
If the side boundary opposite to the vertical wall is located far from the wall, the no-flux boundary condition, Eq. (6), can also be used. However, to save the computational resources the obliquely incident plane wave condition is prescribed along the side boundary at as
Along the outer side no boundary condition is necessary, because Eq. (1) is a parabolic-type differential equation. The grid size, Δx and Δy, is L∕80 where L is the wave length of an incident wave. The size of the computational domain is 50 L in the x direction, and 400 L in the y direction.
For the latter we use the nonlinear parameter, K, proposed by Yue and Mei (1980) and given as
K is the single parameter representing both the nonlinearity of incident wave and the angle of incidence on the formation of stem waves along the vertical wall. This nonlinear parameter was obtained by Yue and Mei (1980) from the dimensionless form of the small angle version of Eq. (1). The details of the derivation of K can be found in Yue and Mei (1980).
2.2 Analytical solution
Chen (1987) developed an analytical solution for the Helmholtz equation in polar coordinates to solve the combined reflection and diffraction of monochromatic waves due to a vertical wedge. The analytical solution is given in a polar coordinate as shown in Fig. 1 as
where is the velocity potential, and is a diffraction factor (i.e., A∕a0) given as
where , , , and θ0 is the angle of incidence. J0(kr) is the Bessel function of the first kind of order 0. The absolute value of the diffraction factor represents the normalized wave amplitude |A|∕a0, or the normalized wave height H∕H0 where H0(=2a0) is the wave height of the incident wave. The analytical solution of Chen (1987) is linear. Thus, this analytical solution does not allow the formation of stem waves. The details of the derivation of the analytical solution can be found in Chen (1987).
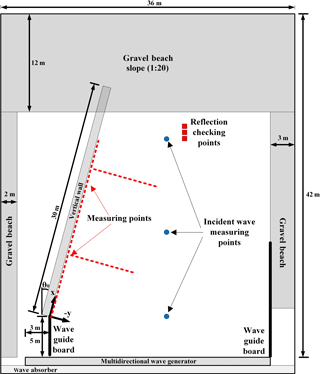
Hydraulic experiments are carried out in the multidirectional irregular wave generation basin of the Korea Institute of Construction Technology (see Fig. 3). The basin used in the laboratory experiments is 42 m long, 36 m wide, and 1.05 m high. A snake-type wave generator consisting of 60 wave boards, each with dimensions of 0.5 m in width and 1.1 m in height and driven by an electronic servo piston, is installed along the 36 m long bottom wall of the wave basin. Free surface displacements are measured using 0.6 m long capacitance-type wave gauges with a measuring range of ±0.3 m.
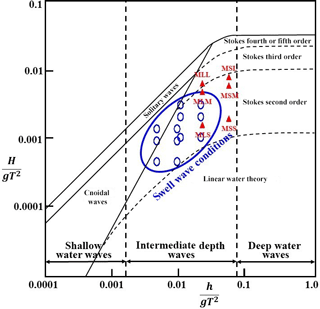
Figure 5The present experiment and wave conditions of the real-world cases (after Le Méhauté, 1976). The solid red triangles represent the incident waves tested in this study and empty blue circles represent the swell wave conditions. The x axis represents the relative water depth (ratio of water depth to deep water wave length, i.e., the measure of wave dispersion). The y axis represents the wave steepness (ratio of wave height to deep water wave length, i.e., the measure of wave nonlinearity).
Figure 4 shows the configuration of the experimental setup and model installation. A 30 m long vertical wall is installed along the left lateral side of the basin in four different orientations. A dissipating gravel beach with a 1∕20 slope is arranged on the opposite side of the wave generator to reduce the reflection of waves inside the basin. Another dissipating beach and wave absorber are also set along the lateral sides and at the back of the wave generator. Along the lateral side opposite to the vertical wall a 10 m long wave guide is installed to avoid diffraction from the side wall. Note that θ0 is the angle between the vertical wall and the incident waves. The origin of the spatial coordinate system of the laboratory experiments (i.e., x0, y0) is set at the tip of the vertical wall which is located 3 m and 5 m away from the lateral side and the wave generator, respectively, as shown in Fig. 4. The width and height of the vertical wall were both 0.6 m. The experiments are carried out at a constant water depth of h=0.25 m. The free board from a still water level to the top of the vertical wall is 0.35 m in order to prevent overtopping of waves.
The incident wave conditions are summarized in Table 1. The title of each test case is composed of three alphabet characters and a numeric digit. The first letter, M, stands for “monochromatic” waves. The letters S or L represents “shorter” or “longer” waves in terms of period, respectively. The letters S, M, or L represents “small”, “medium”, or “large” waves in terms of wave height, respectively. Finally, the numeric digit represents the angle of incidence.
The wave periods of T=0.7 and 1.1 s are tested. The wave heights are H0 = 0.009, 0.027, and 0.036 m for 0.7 s waves and H0 = 0.018, 0.054, and 0.072 m for 1.1 s waves so that no wave breaking occurs during the experiments. The length of the vertical wall in the laboratory experiments is 40 L for the case of T = 0.7 s and 20 L for the case of T = 1.1 s, where L represents the wavelength of monochromatic waves corresponding to the given period T. The incident angles of θ0=10, 20, 30, and 40∘ are obtained by adjusting the orientation of the vertical wall. Thus, the incident waves propagate normal to the line of the wave generator. The nonlinearity of the incident waves are presented in two dimensionless parameters, wave steepness kH0 and the nonlinear parameter K given by Eq. (8).
In the real world, we can assume the situation where the swell is incident on a breakwater. Swell waves are the regular longer period waves created by storms far away from the beach. Swell waves tend to have longer periods than wind waves. The wave period of swell lies between 10 to 15 s. Breakwaters are generally constructed at a depth of about 10 to 20 m. If the wave height is 1 to 3 m, the swell wave conditions can be within the range of Stokes wave, as shown in Fig. 5. In the figure the empty blue circles represent the swell wave conditions and the red triangles represent the incident waves tested in this study. It can be seen that the incident waves tested in this study belong to the Stokes range. The dispersion effect of the Stokes waves is much stronger than that of the solitary waves. Thus, the characteristics of stem waves in this study should be very different from those of the solitary waves. In Fig. 5, the x axis represents the relative water depth (ratio of water depth to deep water wave length, i.e., the measure of wave dispersion). The y axis represents the wave steepness (ratio of wave height to deep water wave length, i.e., the measure of wave nonlinearity).
In the experiments, wave heights are measured along both the vertical wall (x direction) and normal to the vertical wall (y direction). Note that wave heights in the x direction are measured 0.05 m away from the front side of the wall, while wave heights in the y direction are measured along two lines of x = 6 and 15 L. The intervals of the wave height measurement positions are Δx=0.2 m and 0.4 m for T = 0.7 and 1.1 s, respectively, along the wall, and Δy=0.1 and 0.2 m for T=0.7 and 1.1 s, respectively, normal to the wall. Table 2 gives a summary of the wave height measurement positions. The wave heights are extracted from the measured free surface displacements using the zero-upcrossing method. In this method a wave is defined when the surface elevation crosses the zero line or the mean water level upward and continues until the next crossing point. This method is a widely accepted method for extracting representative statistics from raw wave data. Figure 6 shows the hexagonal or beehive wave pattern captured during the experiment in front of a vertical wall for the case of . This is typical of the cross sea generated by the oblique interaction of two or more traveling plane waves (see, e.g., Le Mehauté, 1976; Mei, 1983; Nicholls, 2001). Postacchini et al. (2014) studied the dynamics of crossing wave trains on a plane slope in shallow waters. The stem waves can develop at the intersection of two crest lines of the crossing waves. When the crossing waves propagate towards a shore, they experience shoaling and break. Postacchini et al. (2014) proposed an analytical theory based on ray convergence to identify the position and the crest length of the breaker. The stem waves in the present study are developed by the oblique nonlinear interaction between the incident and the reflected waves. Thus, the generation mechanism is similar to Postacchini et al. (2014).
Prior to the main experiments the performance of the wave generator was tested. For this test no vertical wall was placed in the wave basin. After the initiation of wave generation the time histories of free surface displacement were recorded at three incident-wave-measuring points, as shown in Fig. 4. The first part of data with a sufficiently long time is discarded in evaluating the wave height to avoid the start-up transients, and the wave height and period are obtained using the zero-upcrossing method. The tests show that the target waves are well generated, and that the bottom friction is negligible within the test area of the wave basin. In particular, three wave gauges aligned in a wave propagation direction with a specified distance are placed at the incident-wave-measuring point located near the gravel beach with a 1∕20 slope to estimate the wave reflection from the beach. The incident and reflected waves are separated using the three-point higher-order separation technique. This higher-order technique is developed for finite-amplitude waves by adding the second and third harmonics to the linear separation scheme proposed by Suh et al. (2001). The reflection coefficient due to the gravel beach is less than the maintained 3 % for all the waves considered in the experiments.
In this study, experiments on the formation of stem waves near a vertical wall are conducted and the measured wave heights are compared with results calculated using both the wide-angle parabolic approximation equation numerical model, REF/DIF, and the analytical solution of Chen (1987). All the figures for the experimental and calculated data are presented in the Supplement to avoid an excess of figures.
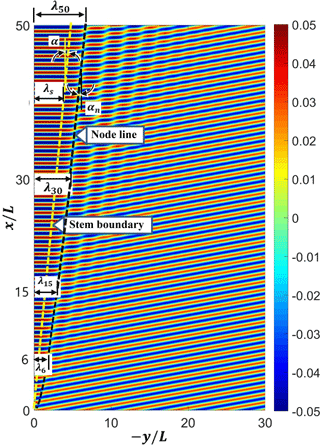
Prior to presenting the experimental and numerical results, the definitions of the stem angle and the stem width are discussed. The definition of stem width is rather controversial. Yue and Mei (1980) defined the stem width as the distance from the wall to the edge of the uniform wave amplitude region. However, it is not an easy task to locate the edge of the flat region. Berger and Kohlhase (1976) defined the stem width for the periodic waves as the distance along the stem crest lines from the wall to the first node line of the standing wave pattern, which is easier to identify from the measured data. However, Soomere (2004) obtained the analytical stem length using the KP equation for the obliquely interacting two solitary waves. As pointed out by Li et al. (2011) the crest lines of the stem wave, the incident, and the reflected solitons measured in their experiment are not straight, and they do not meet at a point. In reality, the analytical solutions of the KP equation deviate slightly from the pattern observed in the experiment. Thus, Li et al. (2011) proposed the edge of the Mach stem as the intersection of the linear extensions of the stem and the incident-wave crest lines.
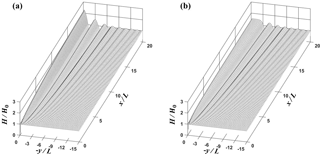
Figure 8Three-dimensional plots of normalized wave height for (a) MLS1 and (b) MLL1 cases from simulation.
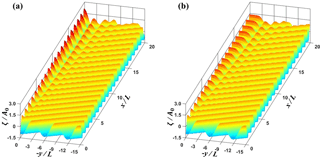
Figure 9Three-dimensional plots of normalized free surface displacements (a) MLS1 and (b) MLL1 cases from simulation.
For the periodic waves the wave pattern is more complicated because many wave components are superposed. Thus, the definitions of the stem boundary and the stem angle should be different from the case of solitary waves. As shown in Figs. 2a and 7, when the stem waves are fully developed, the stem boundary is nearly parallel to the first node line. Thus, as suggested by Berger and Kohlhase (1976), the experimental stem angle α is determined in this study as the angle of node line, αn. The node line is roughly determined using the node points from the wave height data measured along two lines of x = 6 and 15 L. When the distances between the first node points and the wall are λ6 and λ15 for two sections of x = 6 and 15 L, respectively (see Figs. S5 and S6), then the angle of the node line, αn, can be determined as
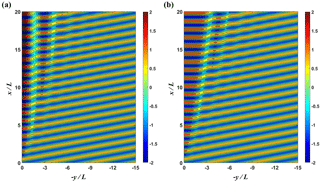
Figure 10Contour plots of the instantaneous normalized free surface for (a) MLS1 and (b) MLL1 cases from simulation.
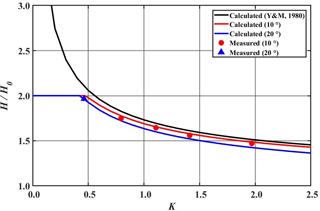
Figure 11Comparison of calculated and measured normalized wave heights along the wall as a function of nonlinear parameter K. Black solid curve represents the wave height predicted by shock theory of Yue and Mei (1980), red and blue solid curves denote the calculated wave heights for θ0=10 and 20∘, respectively. Symbols are measured data.
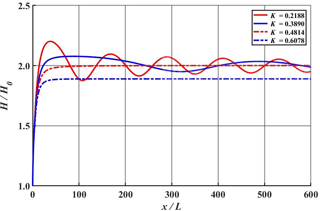
Figure 12Comparison of calculated normalized wave heights along the wall for various nonlinear parameter values of K ().
This αn decreases as the waves propagate along the wall. It reaches an asymptotic value after the waves propagate approximately 30 wave lengths. Thus, the experimental αn determined by Eq. (11) is slightly overestimated for x≤30L.
In this study the stem angle, α, is defined as the asymptotic angle of node line as shown in Fig. 7. To estimate the asymptotic αn the numerical calculation is conducted using the domain extended up to 50 L in the x direction, and the instantaneous free surface displacements are calculated and plotted as shown in Fig. 7. Using two distances between the node points and the wall, λ30 and λ50 for two sections of x = 30 and 50 L, respectively, the stem angle α is determined as
The stem width λs can be determined using the stem angle α as
4.1 Shorter waves (T = 0.7 s)
Figure S1 shows the comparisons between the measured, numerically simulated, and analytically calculated wave heights, H ∕ H0, along the vertical wall for the cases of H0 = 0.009 m with T = 0.7 s (i.e., MSS series). The amplitude of the incident waves is small, as the title of the test cases indicates. The solid circles represent the results of the laboratory experiments. The solid and dashed lines represent the numerical (using REF/DIF) and analytical solution results, respectively. Various incident angles of θ0=10, 20, 30, and 40∘ are presented. For the case of small angle of incidence (MSS1, θ0=10∘) the measured wave height along the vertical wall increases monotonically with the distance from the tip of the vertical wall. As the angle of incidence increases, the wave height shows a slowly varying undulation with the average value of . The maximum value of undulation is approximately , and the location of maximum wave height decreases with increasing angle of incidence. In particular, the overall pattern of wave height distribution does not support the generation of stem waves, which are characterized by uniform wave heights smaller than those obtained from linear diffraction theory (Yue and Mei, 1980; Yoon and Liu, 1989). The wave heights calculated using the REF/DIF numerical model (Kirby and Dalrymple, 2002) and the analytical solution of Chen (1987) agree well with the measured wave heights. This supports the idea that the effects of nonlinearity of incident waves are too weak to develop stem waves. In the case of , the maximum normalized wave heights does not reach because the size of the experimental area is insufficient. If the vertical wall is sufficiently long, the same result could apparently be obtained for .
Figures S2 and S3 show the comparisons of wave heights H∕H0 along a line (x = 6, 15 L) perpendicular to the vertical wall. The distribution of wave height shows the typical pattern of standing waves formed by superposition of the reflected waves on the incident waves. Berger and Kohlhase (1976) called these standing waves stem waves as long as they propagated parallel to the wall. If stem waves, however, are defined as waves with a uniform wave height in the direction normal to the wall, then the wave height distributions for these small-amplitude waves in MSS series show no sign of stem waves. The wave amplitude for this MSS series is too small to generate stem waves along the wall.
Figure S4 shows normalized wave heights along the vertical wall for the cases of MSM series (i.e., H0 = 0.027 m, T = 0.7 s) with various angles of incidence. The amplitude of the incident waves is 3 times larger than the MSS series waves. Figures S5 and A6 show normalized wave heights perpendicular to the vertical wall at positions x = 6 and 15 L, respectively. The results shown in Fig. S4 indicate that, when the angle of incidence is small (), the normalized wave height approaches a uniform value of as waves propagate along the vertical wall. At larger incident angles, the maximum normalized wave heights reach up to , and showed a slowly varying undulation.
In the results shown in Figs. S5 and S6 the stem waves of uniform wave height are found under the conditions of , x = 6 and 15 L, albeit with small stem widths. However, in the cases of other incident angles, stem waves do not appear. The red lines shown in the figures represent the stem waves. For the stem width λs, the stem angle α is first determined by Eq. (12) using the numerical simulation result with the using extended domain. The stem width λs is then calculated using Eq. (13) for given x.
The results from laboratory experiments are in good agreement with those of the results of REF/DIF model. However, the analytical solutions of Chen (1987) do not agree well with the measured data, probably because of nonlinear interactions between incident and reflected waves. The discrepancy between the analytical solution of Chen (1987) and the measured data decreases as the angle of incidence increases. This can be attributed to the decrease in the intensity of nonlinear interactions between incident and reflected waves as the angle of incidence increases.
Figures S7, S8, and S9 show the comparisons of the measured, numerically simulated, and analytically calculated results for the cases of MSL series (H0 = 0.036 m, T = 0.7 s). The amplitude of the incident waves is the largest among the shorter wave test cases. For the case of small angle of incidence, , the normalized wave height increases monotonically to reach a constant value of , with a strong indication of stem wave development. In the cases of larger angle of incidence the wave heights show a slowly varying undulation. As shown in Figs. S8 and S9, which represent normalized wave heights in the direction normal to the vertical wall, stem waves appear clearly for along x = 6 and 15 L. It can also be seen that the width of stem waves increases in proportion to the distance from the tip of vertical wall. In the cases of larger incidence angles, the normalized wave heights tend to show a distribution pattern similar to that of standing waves normal to the wall.
4.2 Longer waves (T = 1.1 s)
Figures S10, S11, and S12 show comparisons between the measured, numerically simulated, and analytically calculated wave heights H∕H0 along the vertical wall (y=0) and normal to the wall (x = 6 and 15 L) for the cases of H0 = 0.018 m with T = 1.1 s (MLS series). The solid circles represent the results of laboratory experiments. The solid and dashed lines represent the numerical and analytical solutions, respectively. The results from laboratory experiments are in good agreement with those from the analytical solution and numerical model. The amplitude of the MLS incident waves is chosen to provide the same steepness, kH0=0.076, as the MSS waves. Hence, the wave patterns observed in the MSS series (Fig. S1) are similar to the results of the MLS series.
Figure S13 shows normalized wave heights along the vertical wall for the cases of MLM series (H0 = 0.054 m, T = 1.1 s). The incident wave amplitude is twice that of the cases of MSM series, but the MLM series have the same wave steepness kH0 as MSM series. For , the maximum value of the normalized wave height reached the uniform value of , which shows an indication of the development of stem waves. Figures S14 and S15 show normalized wave heights normal to the vertical wall at positions along x = 6 and 15 L for various incident angles. As shown in Figs. S14 and S15, stem waves appear for the cases of . The stem widths increase proportionally with the distance from the tip of the vertical wall. The width of the stem waves is found to decrease as the incident angle increases. The linear analytical solutions for small incident angles show large deviations from the measured results, which is consistent with previous results for the cases of MSM series. However, the simulation results using the REF/DIF model are generally in good agreement with the results from laboratory experiments.
Figures S16, S17, and S18 show comparisons of the measured, numerically simulated, and analytically calculated results of MLL series (H0 = 0.072 m, T = 1.1 s). In the results from the laboratory experiment, stem waves appear clearly at positions along x = 6 and 15 L for and 20∘. Such clearly identifiable stem waves for periodic waves in the physical experiments are observed for the first time in this study. Berger and Kohlhase (1976) also conducted laboratory experiments to produce stem waves with a vertical wall. The experiments of Berger and Kohlhase (1976) were conducted in a constant water depth of h = 0.25 m for the wave length of L = 1.0 m with various incoming wave heights of H0= 0.023 ∼ 0.053 m, and incidence angles of θ0 = 10, 15, 20, and 25∘. The experimental wave conditions of Berger and Kohlhase (1976) are similar to those of this study. The length of vertical wall (less than 9.8 L) used in the experiments of Berger and Kohlhase (1976), however, is much shorter than that of this study (40 L for the case of T = 0.7 s and 20 L for the case of T = 1.1 s). Moreover, both ends of the vertical wall were open in the experiments of Berger and Kohlhase (1976), while a wave guide is installed from the wave generator to the tip of vertical wall in the present experiments, and the other end of the vertical wall is extended to the midst of 1∕20 gravel beach. As a result, the wave heights along the wall measured by Berger and Kohlhase (1976) were contaminated by the parasitic waves diffracted by both ends of the wall. Thus, the stem waves developed along the wall were not clear in the results of Berger and Kohlhase (1976), while the stem waves observed in the present experiments are clearly noticeable.
Figures 8a and b show the comparison of the three-dimensional plots of normalized wave height for MLS1 and MLL1 cases, respectively, based on the numerical results of REF/DIF. For the nonlinear case, the overall amplitudes are much smaller and the stem waves are developed along the wall, as shown in Fig. 8b. The stem wave height is nearly constant and the width of the stem waves tended to increase along the wall. Figure 9a and b present the comparison of the three-dimensional plots of normalized free surface displacements, , for MLS1 and MLL1 cases, respectively. From Fig. 9b it can be seen that the stem waves propagate along the wall. Figure 10 shows the contour plots of the instantaneous normalized free surface for MLS1 and MLL1 cases. The incident waves are reflected from the wall for the linear case. However, for the nonlinear cases, they seem to be both refracted and partially reflected at the edge of stem region, as is also depicted in Fig. 2. The rigorous interpretation of this refraction and partial reflection is that the resonant interaction between the incident and reflected waves generates the stem waves propagating along the wall and also shifts the phase of the reflected waves outward from the stem region.
In conclusion, the results of the laboratory experiments are in good agreement with those of the numerical simulations. However, the analytical solution cannot reproduce the stem waves. In addition, given the same incident angle condition, the stem waves in the cases of MLL series show the largest stem width. Moreover, the widths of the stem waves tend to increase as the nonlinear property of the incident waves increases. This further demonstrates the effect of nonlinearity of incident waves on the development of stem waves as suggested by Yue and Mei (1980) and Yoon and Liu (1989).
4.3 Effects of nonlinearity
Yue and Mei (1980) proposed that a single parameter, K, given by Eq. (8), controls the properties of stem waves developed along a vertical wedge based on the nonlinear Schrödinger equation. The K parameter represents both the nonlinearity of incident waves and the wedge slope. Yue and Mei (1980) also proposed a theoretical formula to estimate the amplitude squared of stem waves based on a simple shock model as
where A∞ is the amplitude of stem waves far from the tip of wedge along the vertical wall, and a0 is the amplitude of incident waves. Thus, |A∞∕a0| represents the amplification ratio of the stem waves. In Fig. 11 the normalized wave height, H∞∕H0, instead of A∞∕a0, along the vertical wall is calculated using Eq. (1) and is compared with both the measured value and the theoretical one given by Eq. (14). A black solid line denotes the theoretical prediction by Yue and Mei (1980), and red and blue solid lines represent the present numerical values for θ0=10 and 20∘, respectively. The amplification curves obtained from the numerical calculations for K≤0.45 take a long distance to reach the asymptotic value of 2 as shown in Fig. 12. Thus, this asymptotic value cannot be realized in the laboratory due to the limitation of the experimental facility. However, for K>0.45 the stem waves are generated and the amplification ratio increases monotonically to reach the asymptotic value in a relatively short distance. The theoretical prediction of Yue and Mei (1980) overestimates slightly the stem heights in comparison with the measured values. The results from the present numerical simulation show good agreement with the measured values. Moreover, the present numerical results show a dependence of stem heights on the angle of incidence. This implies that K is not a unique single parameter to control the property of stem waves. It is interesting to note that the maximum amplification of the stem wave is 2 times that of the incident waves for Stokes waves, while that of solitary waves is 4-fold. This indicates that the resonant interaction between the incident and the reflected waves is weaker for the case of the Stokes waves.
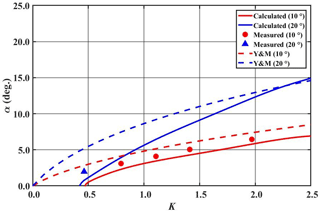
Figure 13Comparison of calculated and measured stem angle α as a function of nonlinear parameter K. Dashed curves represent the calculated values using Yue and Mei (1980), solid curves are the calculated values using Eq. (12), symbols are measured data. Red and blue colors are for θ0=10 and 20∘, respectively.
It is well known that the stem waves are generated by the nonlinear interactions between the incident and the reflected waves. When the angle between the incident and the reflected waves is small and the amplitude of two waves is small but finite, two waves attract each other and form a new wave with a single crest: the so-called stem wave. The amplitude of the stem wave is larger than the incident wave, and that of the reflected wave is smaller. Three waves meet at a point due to both the continuous growth of the crest length of the stem wave and the phase shift of the reflected wave. All the mechanisms observed in the formation of a Mach stem wave for the solitary waves also apply for the monochromatic Stokes waves, but the intensity of nonlinear interaction is weaker than that of solitary waves.
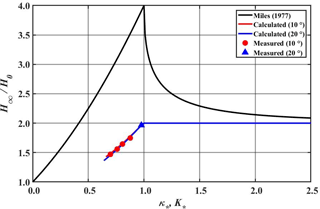
Figure 14Comparison of amplification ratios, H∞∕H0, as a function of nonlinear parameter κ∗ for solitary waves and K∗ for Stokes waves. Black solid curve represents the Miles' solution for solitary waves, red and blue solid curves denote the calculated values for Stokes waves for and 20∘, respectively. Symbols are measured data for Stokes waves.
Yue and Mei (1980) proposed the slope ratio β of the edge line, i.e., stem boundary, of the stem region denoted by a black dashed line in Fig. 2b as a function of K as follows:
This slope ratio β of Yue and Mei (1980) can be converted to the angle of stem wedge α as follows:
where βϵ is the slope of the stem boundary as shown in Fig. 2b. Figure 13 shows the comparison of the α values evaluated using Eq. (16) of Yue and Mei (1980) and those determined from the numerical simulation using Eq. (12), along with the measured data determined using Eq. (11). The theoretical prediction of Yue and Mei (1980) generally overestimates the stem angle. In particular, the numerical simulations and experiments show no stem wave for the range of small K less than 0.46, while the prediction of Yue and Mei (1980) still gives a nonzero stem angle. The stem angles measured in the present experiment are slightly larger than those of the numerical simulation, because the experimental values are obtained in the development stage.
The characteristics of stem waves developed by monochromatic Stokes waves investigated in this study are compared with those of the solitary waves.
For comparison purposes the amplification ratio, H∞∕H0, predicted by Miles (1977) for solitary waves is calculated using the interaction parameter, ), modified by Kodama et al. (2009) as
The interaction parameter κ∗ is inversely proportional to , while the parameter K is proportional to . To properly compare the nonlinear effects on the generation of stem waves a new parameter K∗ for Stokes waves is proposed as
where γ is an arbitrary constant to adjust the scale of K∗. By taking γ=0.828 for , and γ=0.805 for the critical condition that divides the regular and Mach reflections locates at for Stokes waves. Figure 14 shows the comparison between the amplification ratios for the present Stokes waves and the solitary waves. A black solid line denotes the amplification ratio calculated using Eq. (17) for solitary waves, while red and blue solid lines represents the amplification ratios obtained from numerical computations for the Stokes waves. The symbols denote the measured amplification ratios. As shown in the figure the amplification ratios for the Stokes waves are much smaller than those of solitary waves. And the maximum amplification ratio for the Stokes waves is 2, while that of solitary waves is 4. This indicates that the intensity of the resonant interaction between the incident and the reflected waves is much weaker than the case of the solitary waves due to strong frequency dispersion.
In this study, precisely controlled experiments are conducted to investigate the existence and the properties of stem waves developed along a vertical wedge for the cases of monochromatic Stokes waves. Numerical and analytical solutions are also obtained and compared with the measured data. The results obtained from this study are summarized as follows.
-
For small-amplitude waves, the wave height along the wall shows slowly varying undulations with the average value of . The maximum value of an undulation is approximately , and the distance from the tip to the location of maximum wave height decreases with increasing angle of incidence. Normalized wave heights perpendicular to the wall show a standing wave pattern. In particular, the wave height distributions for these small-amplitude waves show no sign of stem waves. Both numerical and linear analytical solutions agree reasonably well with measured wave heights.
-
As the amplitude of incident waves increases, the undulation intensity decreases along the wall. For larger-amplitude waves with smaller angle of incidence, i.e., larger K values, the measurements show clear stem waves along the wall. Numerical simulation results are in good agreement with the results of laboratory experiments, while the analytical solution gives no stem wave, because it is linear.
-
Stem waves can develop when the nonlinear parameter K is greater than approximately 0.46. As the nonlinear parameter K increases, the normalized stem height decreases and the stem width increases.
-
The resonant interactions between the incident and reflected waves predicted for solitary waves are not observed for the periodic Stokes waves. The amplification ratios along the wall do not exceed 2 for the case of Stokes waves, while those can reach 4-fold for the solitary waves.
-
The existence and the properties of stem waves for sinusoidal waves found theoretically via numerical simulations are favorably supported by the physical experiments conducted in this study. Experimental data obtained in this study can be used as a useful tool to verify nonlinear dispersive wave numerical models.
All figures for the experimental and calculated data are presented in this supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/npg-25-521-2018-supplement.
The authors declare that they have no conflict of interest.
This study was performed by a project of “Investigation of large swell waves
and rip currents and development of the disaster response system (No.
20140057)” sponsored by the Ministry of Oceans and Fisheries of
Korea.
Edited by: Victor Shrira
Reviewed by: Tarmo Soomere and four anonymous referees
Berger, U. and Kohlhase, S.: Mach-reflection as a diffraction problem, Proc. 15th Conf. Coastal Eng., Honolulu, Hawaii, July 1976, 796–814, 1976.
Chen, H. S.: Combined reflection and diffraction by a vertical wedge, Tech. Rep. CERC 87-16, US Army Corps of Engrs. (USACE) Wtrwy. Experiment Station, Vicksburg, Miss., USA, 1987.
Gidel, F., Bokhove, O., and Kalogirou, A.: Variational modelling of extreme waves through oblique interaction of solitary waves: application to Mach reflection, Nonlin. Processes Geophys., 24, 43–60, https://doi.org/10.5194/npg-24-43-2017, 2017.
Kadomtsev, B. and Petviashvili, V.: On the stability of solitary waves in weakly dispersing media, Sov. Phys. Dokl, 539–541, 1970.
Kirby, J. T.: Large-angle parabolic equation methods, Proceedings of the 20th International Conference on Coastal Engineering, Taipei, November, 410–424, 1986.
Kirby, J. T. and Dalrymple, R. A.: Combined refraction/diffraction model REF/DIF 1, Version 3.0: Documentation and User's Manual, Center for Applied Coastal Research, Department of Civil Engineering, University of Delaware, Delaware, USA, 2002.
Kodama, Y.: KP solitons in shallow water, J. Phys. A: Mathematical and Theoretical, 43, 434–484, 2010.
Kodama, Y., Oikawa, M., and Tsuji, H.: Soliton solutions of the KP equation with V-shape initial waves, J. Phys. A, 42, 312–321, 2009.
Lee, J. and Kim, Y.: Numerical analysis of stem waves along a vertical wall, J. Coast. Res., 1101–1105, 2007.
Lee, J. I. and Yoon, S. B.: Hydraulic and numerical experiments of stem waves along a vertical wall, J. Korean Soc. Civil Eng., 26, 405–412, 2006.
Lee, J.-I., Kim, Y.-T., and Cho. Y.-S.: Hydraulic model test for stem waves along vertical wall under regular wave actions, Proc. of Annual Conf. of Korean Society of Civil Engineers, October 2003, Daegu, Korea, 4939–4943, 2003.
Le Mehaute, B.: An introduction to hydrodynamics and water waves, Springer, New York, 525 pp., 1976.
Li, W., Yeh, H., and Kodama, Y.: On the Mach reflection of a solitary wave: revisited, J. Fluid Mech., 672, 326–357, 2011.
Liu, P. L. F. and Yoon, S. B.: Stem waves along a depth discontinuity, J.Geophys. Res.-Oceans, 91, 3979-3982, 1986.
Melville, W.: On the mach reflexion of a solitary wave, J. Fluid Mech., 98, 285–297, 1980.
Mei, C. C., Stiassnie, M., and Yue, D. K.-P.: Theory and applications of ocean surface waves: Part 1: Linear aspects Part 2: Nonlinear aspects, World Scientific, Singapore, 809–816, 2005.
Miles, J. W.: Obliquely interacting solitary waves, J. Fluid Mech., 79, 157–169, 1977a.
Miles, J. W.: Resonantly interacting solitary waves, J. Fluid Mech., 79, 171–179, 1977b.
Nicholls, D. P.: On hexagonal gravity water waves, Math. Comp. Sim., 55, 567–575, 2001.
Perroud, P. H.: The solitary wave reflection along a straight vertical wall at oblique incidence, IER Report. 99-3, 93, University of California, Berkeley, California, USA, 1957.
Postacchini, M., Brocchini, M., and Soldini, L.: Vorticity generation due to cross-sea, J. Fluid Mech., 744, 286–309, 2014.
Soomere, T.: Interaction of Kadomtsev-Petviashvili solitons with unequal amplitudes, Phys. Lett. A, 332, 74–81, 2004.
Suh, K. D., Park, W. S., and Park, B. S.: Separation of incident and reflected waves in wave–current flumes, Coast. Eng., 43, 149–159, 2001.
Yoon, S. B. and Liu, P. L.-F.: Stem waves along breakwater, J. waterway, Port Coast. Ocean Eng., 115, 635–648, 1989.
Yue, D. K. and Mei, C. C.: Forward diffraction of Stokes waves by a thin wedge, J. Fluid Mech., 99, 33–52, 1980.