the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Fluctuations of finite-time Lyapunov exponents in an intermediate-complexity atmospheric model: a multivariate and large-deviation perspective
The stability properties as characterized by the fluctuations of finite-time Lyapunov exponents around their mean values are investigated in a three-level quasi-geostrophic atmospheric model with realistic mean state and variability. Firstly, the covariance structure of the fluctuation field is examined. In order to identify dominant patterns of collective excitation, an empirical orthogonal function (EOF) analysis of the fluctuation field of all of the finite-time Lyapunov exponents is performed. The three leading modes are patterns where the most unstable Lyapunov exponents fluctuate in phase. These modes are virtually independent of the integration time of the finite-time Lyapunov exponents. Secondly, large-deviation rate functions are estimated from time series of finite-time Lyapunov exponents based on the probability density functions and using the Legendre transform method. Serial correlation in the time series is properly accounted for. A large-deviation principle can be established for all of the Lyapunov exponents. Convergence is rather slow for the most unstable exponent, becomes faster when going further down in the Lyapunov spectrum, is very fast for the near-neutral and weakly dissipative modes, and becomes slow again for the strongly dissipative modes at the end of the Lyapunov spectrum. The curvature of the rate functions at the minimum is linked to the corresponding elements of the diffusion matrix. Also, the joint large-deviation rate function for the first and the second Lyapunov exponent is estimated.
The atmosphere is a high-dimensional non-linear chaotic dynamical system; its time evolution is characterized by sensitivity to initial conditions (Lorenz, 1963; Kalnay, 2003). As a consequence predictability is limited; small errors in the initial states progressively grow under the time evolution until the forecast eventually becomes useless, that is, it is indistinguishable from the invariant measure or climatology of the system. Understanding the structure of this inherent instability is key to improve forecasts at all timescales.
Sensitivity to initial conditions and perturbation growth in non-linear dynamical systems are often quantified using Lyapunov exponents (LEs; e.g. Eckmann and Ruelle, 1985; Ott, 2002; Pikovsky and Politi, 2016). They describe the asymptotic growth or decay of infinitesimal perturbations. A system is chaotic if it has at least one positive Lyapunov exponent. However, the predictability properties may vary substantially across state space. Finite-time (or local) Lyapunov exponents (FTLEs) allow a characterization of the stability of a particular initial state with respect to a predefined prediction horizon.
LEs have been calculated for various geophysical fluid systems, ranging from highly truncated atmospheric models (Legras and Ghil, 1985), to intermediate-complexity atmospheric models (Vannitsem and Nicolis, 1997; Schubert and Lucarini, 2015) and coupled atmosphere–ocean models (Vannitsem and Lucarini, 2016). A review has been published recently by Vannitsem (2017). Models tuned to realistic conditions were found to possess quite a large number of positive LEs corresponding to a high-dimensional chaotic attractor.
The present paper investigates the fluctuations of FTLEs in an intermediate-complexity atmospheric model with realistic mean state and variability. It focuses on two aspects that have found little attention in the context of geophysical fluid systems thus far. Firstly, the covariance structure of the fluctuation field of the FTLEs is studied by means of a principal component (PC) or empirical orthogonal function (EOF) analysis (Kuptsov and Politi, 2011). Secondly, we look at the large-deviation behaviour of the FTLEs (Kuptsov and Politi, 2011; Laffargue et al., 2013; Johnson and Meneveau, 2015). A large-deviation principle links the FTLEs at long integration times to the global LEs by providing a universal law for the probability density of fluctuations of the FTLEs around the mean value. It can be expected to hold for Axiom A dynamical systems and, invoking the chaotic hypothesis, also for certain types of non-Axiom A systems. In particular, a large-deviation law allows one to determine the probability of very stable or very unstable atmospheric states.
The paper is organized as follows: in Sect. 2 the atmospheric model is described; the methodology, which consists of calculating LEs, the multivariate fluctuation analysis and the large-deviation theory, is outlined in Sects. 3, 4 and 5; the results are presented and discussed in Sect. 6; and some conclusions are drawn in Sect. 7.
A quasi-geostrophic (QG) three-level model on the sphere, formulated in pressure coordinates, is used here as dynamical framework. The model is identical to that introduced by Kwasniok (2007) except for the horizontal resolution and the coefficient of hyperviscosity. A very similar model was introduced by Marshall and Molteni (1993). The dynamical equations are as follows:
where Ψi and qi are the stream function and the potential vorticity at level i, respectively, and J denotes the Jacobian operator on the sphere. All variables are non-dimensional using the radius of the Earth as the unit of length and the inverse of the angular velocity of the Earth as the unit of time. The three pressure levels are located at 250, 500 and 750 hPa. Potential vorticity and the stream function are related by
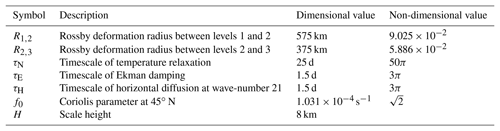
where ∇ is the horizontal gradient operator, and f is the Coriolis parameter. The Rossby deformation radii R1,2 and R2,3 have dimensional values of 575 and 375 km, respectively. The function represents a non-dimensional topography which is related to the actual dimensional topography of the Earth by , where H is a scale height set to 8 km, and f0 is the Coriolis parameter at an average geographic latitude taken to be 45∘ N.
The dissipative terms are given as follows:
They are Newtonian temperature relaxation with a radiative timescale of τN=25 d, Ekman damping on the lowest level with a spin-down timescale of τE=1.5 d, and a strongly scale-selective horizontal diffusion of vorticity and temperature. The is the time-dependent part of the potential vorticity at level i, that is to say . The coefficient of horizontal diffusion is such that harmonics of total wave-number nm=21 are damped at a timescale of τH=1.5 d. The terms are diabatic sources of potential vorticity which are independent of time but spatially varying.
The model is considered on the Northern Hemisphere. The boundary condition of no meridional flow, , that is to say vanishing stream function, , is applied at the Equator on all three model levels. The horizontal discretization is spectral, triangularly truncated at total wave-number nm=21. The number of degrees of freedom is 231 for each level and N=693 in total. The model is integrated in time using the third-order Adams–Bashforth scheme with a constant step size of 1 h.
The variables of the QG model are listed in Table 1; the model parameters are listed in Table 2 with their dimensional and non-dimensional values.
In order to get a model behaviour close to that of the real atmosphere, the forcing terms Si are determined from the European Centre for Medium-Range Weather Forecasts (ECMWF) reanalysis data by requiring that when computing potential vorticity tendencies for a large number of observed atmospheric fields, the average of these tendencies must be zero (Roads, 1987); this is done in order for the ensemble of reanalysis data states to be representative of a statistically stable long-term behaviour of the QG model. The timescale of horizontal diffusion τH is determined such that the slope of the kinetic energy spectrum at the truncation level in the model matches that in the reanalysis data. See Kwasniok (2007) for details on the parameter tuning procedure. The QG model exhibits a remarkably realistic mean state and variability pattern of stream function and potential vorticity in a long-term integration (see Table 3).
Table 1Variables and fields in the QG model and their non-dimensionalization with the Earth's radius and the angular velocity of the Earth .

We consider a non-linear autonomous dynamical system with state vector governed by the evolution equations
The linearized dynamics of a small perturbation δx are given as
The propagation of the perturbation between time t0 with initial state x0=x(t0) and time t (t>t0) can be written as
where M is the resolvent matrix. If the system is ergodic, then according to the theorem by Oseledets (1968) the limit
exists and is the same for almost all initial conditions x0. The (global) LEs are defined as
where are the positive eigenvalues of the matrix S. The set of all LEs, usually presented in non-increasing order, is called the “Lyapunov spectrum”. The LEs are independent of the norm.
In order to characterize perturbation growth or decay over a finite integration time τ the FTLEs are introduced. There are three different definitions of FTLEs. One can compute them by making reference to the backward, forward or covariant Lyapunov vectors – see e.g. Kuptsov and Parlitz (2012) for a review. In the limit of large integration time τ, which is the main focus of the present study, all of the three definitions become more and more equivalent (Kuptsov and Politi, 2011; Pazó et al., 2013). Here, we refer to the backward FTLEs as they are easiest to compute. They are calculated using the standard algorithm based on the Gram–Schmidt orthogonalization (Shimada and Nagashima, 1979; Benettin et al., 1980). An ensemble of N linearly independent perturbations is initialized and integrated forward in time along with the non-linear model trajectory. A transient period is discarded for the trajectory to settle on the attractor of the system and for the perturbations to converge to the backward Lyapunov vectors. Then, after every integration time interval Δτ the perturbations are re-orthonormalized using a QR-decomposition performed via the Gram–Schmidt procedure. The FTLEs are obtained as
where are the diagonal elements of the upper triangular matrix R in the QR-decomposition resulting from the integration between times tα and tα+1. We have and xα=x(tα). The FTLEs for larger integration times τ=nΔτ are obtained by averaging over n consecutive values of :
For all integration times τ, we keep time series of FTLEs of the same length L, , characterizing the stability of the states over the time horizon τ.
The FTLEs depend on the scalar product chosen in the Gram–Schmidt orthogonalization procedure. Here, we use the total energy scalar product with its associated total energy norm (Ehrendorfer, 2000; Kwasniok, 2007). The dependence of the FTLEs on the norm becomes increasingly weaker in the limit of large integration time τ.
The FTLEs are related to the global LEs by
for almost all initial states x0 and
for all τ, where 〈⋅〉 denotes an ensemble average over the attractor of the system which for ergodic systems can be estimated as a mean over a long time series.
The vector of global Lyapunov exponents is defined as and the fluctuation field as . We study the correlations between the fluctuations of the FTLEs; to do this, preferred patterns of collective excitation are extracted. A canonical approach is a principal component (PC) or empirical orthogonal function (EOF) analysis based on the scaled covariance matrix D(τ) defined as
In the limit of large integration time τ we expect convergence to the diffusion matrix D (Kuptsov and Politi, 2011; Pikovsky and Politi, 2016):
The eigenvalues and eigenvectors of the symmetric, positive definite matrix D(τ) are calculated:
The eigenvalues are arranged in non-increasing order. The eigenvectors form an orthonormal system:
The fluctuation field of the FTLEs is expanded as
with . The principal components are uncorrelated and their variance is given by the corresponding eigenvalue:
The steepness or complexity of the eigenvalue spectrum is characterized by the fraction of variance explained by the principal component given as
and the cumulative fraction of variance given as
As a possible further step, one may try to link the covariance structure of the FTLEs with investigations of the angles between the covariant Lyapunov vectors and the degree of entanglement and interaction of the various unstable and stable directions in tangent space (Yang et al., 2009). This is related to the hyperbolicity and the inertial manifold of the system.
Large-deviation theory (Kifer, 1990; Touchette, 2009) is a powerful approach from statistical physics for estimating the probability of rare events with many applications. It has recently been applied to the behaviour of FTLEs at long integration times (Kuptsov and Politi, 2011; Laffargue et al., 2013; Johnson and Meneveau, 2015). In the following, large-deviation theory is briefly described in the form in which it is used in the present study.
5.1 Univariate theory
For a sequence of n identically distributed but not necessarily independent random variables, , the sample mean
is an unbiased estimator of and converges to the true mean, 〈X〉, as n→∞. According to the Gärtner–Ellis theorem (Touchette, 2009), if the scaled cumulant generating function (SCGF)
exists and is differentiable everywhere, then An follows a large-deviation principle,
where the large-deviation rate function I(z) is independent of n and given as the Legendre–Fenchel transform of the SCGF:
The rate function I(z) is non-negative and strictly convex. It has a unique zero and minimum at , that is to say I(〈X〉)=0 and . The curvature of the rate function at the minimum is given as (Touchette, 2009)
In view of Eq. (14), FTLEs immediately lend themselves to large-deviation theory. For large integration time τ, one would expect the probability density of the FTLE to follow a large-deviation principle,
where the large-deviation rate function Ij(z) is independent of τ and given as
with the SCGF
Introducing and then dropping the prime again we get
We expect convergence of the rate function Ij(z) as soon as the integration time τ is large enough for consecutive values of taken over non-overlapping integration time intervals, and , to be independent. This is actually an application of the block averaging method (Rohwer et al., 2015). Note, however, that convergence of the rate function at a particular value of τ here does not guarantee that the probability density function is already in the large-deviation limit at that value of τ.
The rate function Ij(z) has a unique zero and minimum at , that is to say Ij(λj)=0 and . The curvature of the rate function at the minimum is linked to the diffusion matrix D as
A second-order Taylor expansion of the rate function in the vicinity of λj,
corresponds to a Gaussian probability density with mean λj and variance , recovering the central limit theorem (CLT) as a limit case of large-deviation theory.
5.2 Estimating the rate function
There are two ways of estimating the rate functions Ij(z) from data: via the probability density function (cf., Eq. 30) or via the Legendre transform (cf., Eq. 33).
5.2.1 Probability density function approach
By inverting Eq. (30) we have
We take a maximum likelihood approach for estimating the rate function. The probability density of is modelled as
with normalization constant
The potential function is expanded into a polynomial basis in standardized variables:
Here is the standard deviation of the FTLE :
The parameter M determines the complexity of the model. In order to have a normalizable probability density, we need M to be even and . The expansion coefficients are determined by maximizing the likelihood function of the data . This is a convex optimization problem with a unique maximum which is numerically stable to solve. Model selection is performed with the Bayesian information criterion.
The estimate of the rate function is given as
where z∗ denotes the position of the minimum of the potential function . Note that, for finite τ, we do not necessarily have as the mode of the probability density of may be different from its mean if the distribution is skewed; however, we always have as τ→∞. One would now estimate Ij(z) from the probability density function of for various large values of τ and look for convergence.
The maximum likelihood method tends to provide very smooth and convex rate functions although convexity is not strictly guaranteed. It clearly improves on earlier work (e.g. Johnson and Meneveau, 2015) using histogram or kernel density estimates for the probability density and treating the normalization constant only in the Gaussian approximation.
5.2.2 Legendre transform approach
Alternatively, the rate functions Ij(z) can be determined by numerically implementing the Legendre transform of Eq. (33) (Rohwer et al., 2015) with the moment generating function estimated by the sample mean over the time series:
For each z, this is a convex optimization problem with a unique solution, if a solution exists. Rate functions obtained via the Legendre transform method are guaranteed to be strictly convex with a unique zero and minimum at .
Rate function estimates from the Legendre transform method converge as soon as τ=nΔτ is large enough for successive values of over non-overlapping integration time intervals, and , to be independent. However, this gives no indication of whether or not the probability density function is actually already in the large-deviation limit. Therefore, here we consider both rate function estimates side by side.
5.3 Estimating the diffusion coefficients
The diffusion coefficients Dj,j can be obtained from both rate function estimates as the inverse of the curvature at the minimum (cf., Eq. 34). They can also be estimated directly from the time series of the FTLEs according to Eq. (17). It can be shown that the estimates from the Legendre transform-based rate function and from the time series are always the same; any differences just stem from the error of the finite-difference approximation of the curvature as the Legendre transform is not available in closed form. For a Gaussian probability density model, that is M=2 in Eq. (39), the diffusion coefficient estimates from the probability density-based rate function and from the time series are exactly the same; otherwise they are different.
5.4 Multivariate theory
The large-deviation analysis can be extended to a multivariate approach (Kuptsov and Politi, 2011; Johnson and Meneveau, 2015). Let Λ(τ) now denote the column vector of any K-dimensional subset of the N FTLEs and λ the corresponding vector of global LEs. We have , where K=N corresponds to the full system and K=1 recovers the univariate analysis. For large integration time τ, the joint probability density function of the K FTLEs would then follow a large-deviation principle,
where the joint large-deviation rate function I(z) is independent of τ and given as the multivariate Legendre–Fenchel transform
The joint rate function I(z) is non-negative and strictly convex. It has a unique zero and minimum at , that is to say I(λ)=0 and at z=λ. The Hessian matrix of the joint rate function at the minimum is linked to the diffusion matrix D as
where D denotes the K×K part of the diffusion matrix corresponding to the K retained FTLEs. A second-order Taylor expansion of the joint rate function in the vicinity of λ,
corresponds to a multivariate Gaussian probability density with mean λ and covariance matrix (τQ)−1, recovering the central limit theorem (CLT).
5.5 Estimating the joint rate function
There are again two ways of estimating the joint rate function from the time series of FTLEs: via the probability density function (cf., Eq. 43) or via the Legendre transform (cf., Eq. 44).
5.5.1 Probability density function approach
By inverting Eq. (43) we get
The probability density of Λ(τ) is modelled as
with normalization constant
The potential function U(τ)(z) is expanded into suitable multinomial basis functions as
subject to appropriate conditions to ensure a normalizable probability density. The expansion coefficients are determined from the time series of the FTLEs via maximum likelihood which is a convex optimization problem with a unique solution.
The estimate of the joint rate function is
where z∗ denotes the position of the minimum of the potential function U(τ)(z) which for finite τ is not necessarily equal to λ.
5.5.2 Legendre transform approach
Alternatively, the joint rate function I(z) can be determined via the multivariate Legendre transform of Eq. (44) with the moment generating function estimated as the sample mean over the time series:
Again, this is a convex optimization problem and rate functions obtained from the Legendre transform method are guaranteed to be strictly convex with a unique zero and minimum at .
5.6 Estimating the diffusion matrix
The diffusion matrix D (or the part of it corresponding to the K considered FTLEs) can be obtained from both joint rate function estimates as the inverse of the Hessian matrix at the minimum (cf., Eq. 45). It can also be estimated directly from the time series of the FTLEs as given in Eq. (17). The estimates from the Legendre transform-based joint rate function and from the time series are always the same, apart from errors in the finite-difference approximation of the second derivatives. The diffusion matrix estimates from the probability density-based joint rate function and from the time series are the same if the model in Eq. (50) is a multivariate Gaussian probability density; otherwise they are different.
The different methods for estimating the rate function and the diffusion matrix in the univariate and the multivariate case are summarized in Tables 4 and 5.
In high-dimensional systems it is usually too ambitious a task to determine I(z) beyond the Gaussian approximation for the full system. Here, we restrict ourselves to the bivariate case K=2.
6.1 Lyapunov exponents
Time series of FTLEs of the QG model of length L=25 000 with a basic integration time Δτ=1 d are generated as described in Sect. 3. The (global) LEs are calculated as
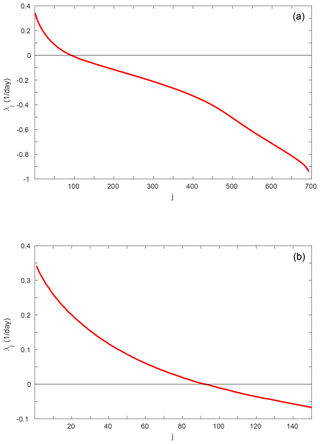
Figure 1 displays the Lyapunov spectrum of the QG model. There are 91 positive LEs. The largest LE is estimated as λ1=0.342 d−1, corresponding to an e-folding time of perturbation growth of 2.9 d which appears to be realistic for the real atmosphere. The spectrum starts off quite steep and then flattens at the near-zero exponents. For example, there are 69 LEs between 0.05 and −0.05 d−1. The spectrum becomes steeper again at the trailing very stable exponents. Overall, there is a continuous spectrum of timescales with no clear timescale separation. This is in accordance with previous results for QG models (Vannitsem and Nicolis, 1997; Schubert and Lucarini, 2015) and is probably because QG equations are scale-filtered equations.
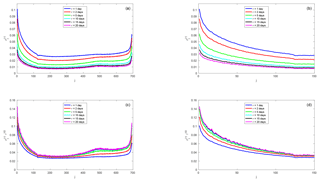
Figure 2(a) Standard deviation of the FTLEs. (b) Close-up of (a). (c) Scaled standard deviation of the FTLEs. (d) Close-up of (c).
Figure 2 shows the standard deviation of the fluctuations of the FTLEs around their mean values (Eq. 40). The standard deviation monotonically decreases with increasing integration time τ for all exponents. The fluctuations are largest for the leading LEs and then quickly decrease. They increase again towards the end of the Lyapunov spectrum with a particularly sharp increase for the most stable exponents at the very end of the spectrum. This is in line with similar findings in simple spatially extended systems (Kuptsov and Politi, 2011; Pazó et al., 2013) as well as in a QG atmosphere–ocean model (Vannitsem and Lucarini, 2016).
The scaled standard deviation shows clear convergence for all of the exponents at τ=10–15 d, that is to say the scaled variance converges to the diagonal elements Dj,j of the diffusion matrix D. Convergence is reached at about τ=10 d for almost all of the exponents; it is particularly fast for the near-neutral and the weakly dissipative exponents where it is already reached at τ=5–10 d.
There is a kink-like feature at j≈125, separating regions with different slopes of the standard deviation. It is possible that this is linked to a distinction of the covariant Lyapunov vectors into interacting “physical modes” and hyperbolically separated “isolated modes” (Yang et al., 2009). But this certainly needs further investigation.
6.2 Multivariate fluctuation analysis
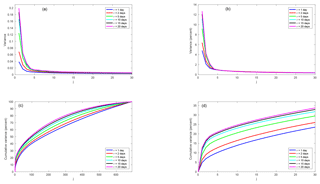
Figure 3(a) Variance of the principal components of the finite-time Lyapunov fluctuations. (b) Fraction of variance. (c) Cumulative fraction of variance. (d) Close-up of (c).
Figure 3 shows the explained variance and the cumulative explained variance of the principal components of the scaled Lyapunov fluctuations. There are three leading modes, then the eigenvalue spectrum sharply flattens off. The fraction of variance explained by the leading modes increases with increasing integration time τ. Going from τ=1 to τ=20 d, the variance explained by the first principal component increases from just below 5 % to more than 12 %, and the variance explained by the second principal component increases from about 2 % to more than 4 %. However, due to the flatness of the bulk of the eigenvalue spectrum, even in the diffusion limit a substantial number of modes is necessary to explain large parts of the fluctuation variance. The eigenvalue spectrum is still not fully converged at τ=20 d. It is not completely clear what the reason for this is. There may be some indication that the off-diagonal elements of the diffusion matrix converge slightly more slowly than the diagonal elements. But there is probably also a finite sample size effect. With increasing τ, the time series of the FTLEs contain less and less uncorrelated information and fail to fully sample the high-dimensional covariance matrix which leads to an overestimation of the variance of the leading principal components.
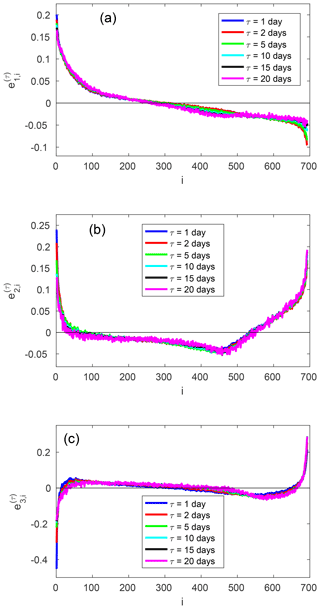
Figure 4(a) First, (b) second and (c) third normalized empirical orthogonal function (EOF) of the finite-time Lyapunov fluctuations (cf., Eq. 20).
In Fig. 4 the three leading EOFs are displayed. The modes are largely independent of the integration time τ and have converged at about τ=10 d. The first EOF shows a pattern where all of the leading FTLEs fluctuate in phase. This incorporates all of the positive exponents and extends to the weakly dissipative ones. Then there is some negative correlation with the dissipative exponents in the second half of the Lyapunov spectrum. In the second EOF, the leading FTLEs again fluctuate in phase; here, this encompasses about the first 40 exponents. Then there is some negative correlation with the weakly dissipative exponents and substantial positive correlation with the strongly dissipative exponents at the end of the Lyapunov spectrum. The third EOF has the very stable exponents at the end of the spectrum fluctuating in phase and the most unstable exponents fluctuating in phase with each other, out of phase with the dissipative ones.
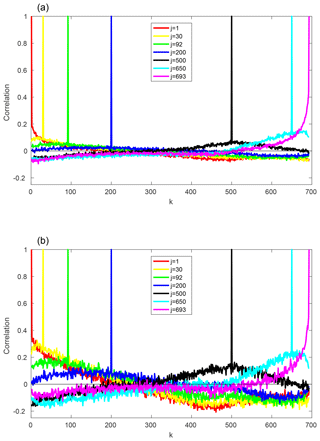
Complementary to the EOF analysis, Fig. 5 shows the correlation of selected FTLEs with each of the other FTLEs for τ=1 and τ=15 d. The pattern of the correlations is the same for both integration times but the amplitudes are very low for τ=1 d and build up at larger integration times. This is in line with the results from the EOF analysis. The FTLEs have predominantly positive correlations with neighbouring exponents; these are strongest for the most unstable and the most stable exponents and weaker in between. There are also some relatively weak long-range correlations across the Lyapunov spectrum.
6.3 Large-deviation analysis
6.3.1 One-dimensional approach
We now investigate whether the fluctuations of the FTLEs obey a large deviation principle. As representative examples we look at the first and the fifth exponent as two strongly unstable modes, at the zero exponent, at a weakly dissipative exponent and at the smallest, most stable exponent. The large-deviation rate function is estimated as described in Sect. 5 from the probability density function and via the Legendre transform for various values of τ. The corresponding element Dj,j of the diffusion matrix is calculated from the curvature of the two estimates of the rate function and directly from the time series of the FTLEs.
To model the probability density of the FTLEs two different choices for the potential function in Eq. (39) are considered here: M=2, this is to say a Gaussian probability density, and M=4, a fourth-order polynomial. In view of the high degree of correlation in the time series of the FTLEs, particularly for large τ, model selection is performed here as follows. For τ=nΔτ, the time series of the FTLEs, , are sub-sampled into n disjoint time series with non-overlapping integration time intervals, , for . The length of the sub-sampled time series is the largest integer L′ such that . The two probability density models are fitted separately on the n sub-sampled time series and model selection is based on the average Bayesian information criterion. Then the selected model is fitted on the whole time series.
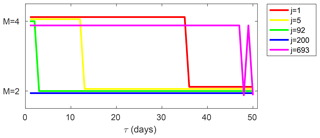
Figure 6 displays the order of the model for the probability density of the selected FTLEs as a function of the integration time τ. The leading unstable exponents exhibit strong non-Gaussianity. For the first exponent, it is detectable up to τ=35 d; for the fifth exponent, it is less pronounced and visible only up to τ=12 d. The zero exponent shows only very mild non-Gaussianity which is visible for τ=1 and τ=2 d. The weakly dissipative exponent has Gaussian behaviour at all values of τ. The smallest, strongly dissipative exponent again displays marked deviations from Gaussianity; these are even more pronounced than those for the first exponent and detectable up to an integration time as large as τ=49 d. For the first and the last exponent, at small integration times τ it may be possible to even switch to the higher-order model M=6 but this is not our concern here.
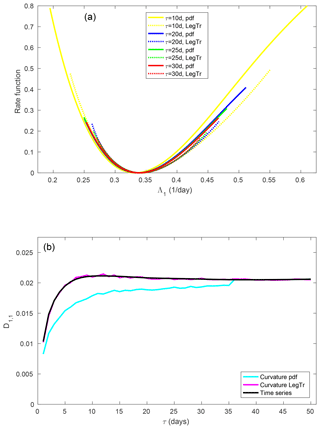
Figure 7(a) Large-deviation rate function of the first FTLE. (b) Element D1,1 of the diffusion matrix.
Figure 7 shows the results of the large-deviation analysis for the first FTLE. Convergence to a large-deviation principle is observed. At τ=10 d and even visible at τ=20 d the maximum of the probability density is still shifted away from the mean; nevertheless, some convergence among the probability density-based estimates of the rate function is reached at about τ=20 d. The Legendre transform-based estimates already give a consistent picture from τ=10 d. Good convergence is also observed for the corresponding element of the diffusion matrix.
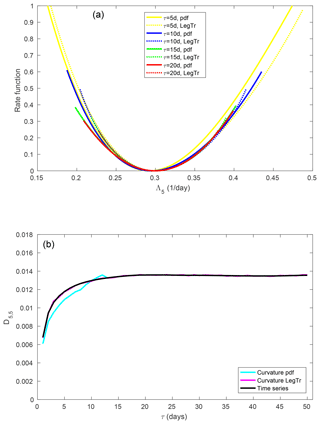
Figure 8(a) Large-deviation rate function of the fifth FTLE. (b) Element D5,5 of the diffusion matrix.
For the fifth FTLE, a similar picture can be seen (Fig. 8) but convergence is markedly faster than for the first FTLE. The probability density-based estimates are very consistent from τ=10–15 d; note that the model for the probability density jumps from fourth-order to Gaussian for the higher values of τ. The Legendre transform already gives close agreement for the rate function from τ=5 d.
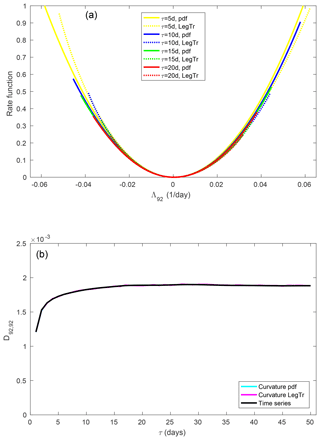
Figure 9(a) Large-deviation rate function of the 92th FTLE. (b) Element D92,92 of the diffusion matrix.
For the zero exponent (Fig. 9), convergence is again markedly faster than for both positive exponents. A large-deviation principle can already be established from about τ=10 d, and the two different estimates of the rate function are close together. The estimates of the diffusion coefficient all coincide.
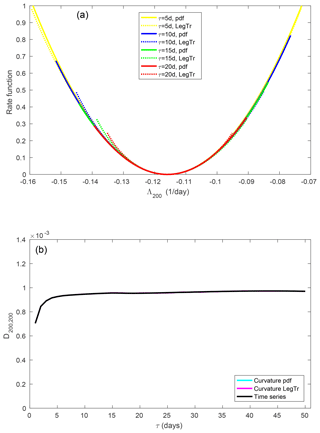
Figure 10(a) Large-deviation rate function of the 200th FTLE. (b) Element D200,200 of the diffusion matrix.
For the fully Gaussian 200th FTLE (Fig. 10), convergence is even faster. A large-deviation principle is valid from τ=5 d and all of the estimates of the rate function are in almost perfect agreement. The estimates of the diffusion coefficient show corresponding behaviour.
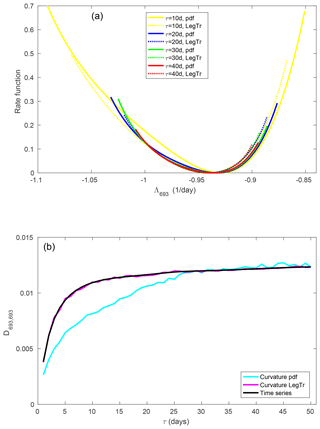
Figure 11(a) Large-deviation rate function of the 693th FTLE. (b) Element D693,693 of the diffusion matrix.
For the smallest, most dissipative exponent (Fig. 11), the convergence to a large-deviation principle is very slow, even slower than for the first, most unstable exponent. A large-deviation principle is valid from about τ=30 d, and the Legendre transform method gives reliable estimates of the rate function from τ=10 to 20 d. Also, the convergence of the diffusion coefficient is markedly slow. The estimate from the non-Gaussian probability density is initially too low and converges at about τ=25 d.
The different speeds of convergence to a large-deviation principle for the different FTLEs can be understood from the degrees of serial correlation and non-Gaussianity of the FTLEs. The correlation length of the FTLE is defined as
where is the autocorrelation of the FTLE at lag i. Note that a lag of 1 here refers to two consecutive but non-overlapping integration time intervals of length τ, that is to say is the autocorrelation at lag i of the sub-sampled time series of as introduced above for the model selection of the probability density model, , for . There are n of these which can be used to generate n estimates of and then take the average. The definition of the correlation length of Eq. (54) occurs naturally in the formulation of the CLT for dependent random variables (e.g. Billingsley, 1995) under the assumption of a Markov process that is sufficiently mixing. Now consider two integration times τ1=n1Δτ and τ2=n2Δτ with n1≤n2 and being an integer for simplicity; one could consider a continuous integration time τ in the limit Δτ→0. The variances of and are linked as , and the two estimates of the diffusion coefficient, as calculated from the time series or the Legendre transform, are linked as . This holds in the limit , otherwise needs to be replaced with a counterpart that takes only a finite number of lags into account and also contains some correction terms. Convergence to a large-deviation principle is limited by serial correlation of the FTLEs. Convergence to the diffusion limit, that is to the Gaussian approximation of the large-deviation regime, can certainly not be expected before the serial correlations have decayed, that is to say when . If the distribution of the FTLEs is Gaussian or close to Gaussian the large-deviation limit is equivalent to the diffusion limit and convergence occurs immediately after correlation decay; otherwise it is further delayed, generally the longer the delay the larger the departure from Gaussianity.
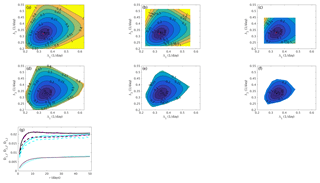
Figure 12Joint large-deviation rate function of the first two FTLEs as estimated from the joint probability density for (a) τ=10 d, (b) τ=15 d and (c) τ=25 d; and with the Legendre transform for (d) τ=10 d, (e) τ=15 d and (f) τ=25 d. Black dots indicate the global LEs (λ1,λ2); and red dots in panels (a), (b) and (c) indicate the maximum of the joint probability density. (g) Elements D1,1 (solid), D2,2 (dashed) and D1,2 (dotted) of the diffusion matrix as estimated from the curvature of the probability density-based rate function (cyan), from the curvature of the Legendre transform-based rate function (magenta) and from the time series of the FTLEs (black).
Table 6 gives the correlation length of the selected FTLEs at the basic integration time Δτ=1 d. Note that does not allow one to directly calculate the value of τ at which convergence to a large-deviation principle occurs but it gives an impression of the timescales of temporal correlation and how they differ for the different FTLEs. Overall, temporal correlation is not very pronounced for all of the FTLEs, but the correlation length varies by a factor of 2.35 from the shortest to the longest. The rapid convergence to a large-deviation principle for the zero and weakly dissipative exponents is in line with their short correlation length and almost Gaussian distribution. For the first and the last exponent convergence is delayed beyond what is expected from the somewhat larger correlation length due to the strong non-Gaussianity .
6.3.2 Two-dimensional approach
As an example of a multivariate large-deviation analysis, Fig. 12 shows the joint large-deviation rate function of the first two FTLEs, Λ1 and Λ2. The estimates of the diffusion coefficients D1,1, D2,2 and D1,2 are also shown. The potential function for the joint probability density is chosen as
where the order of the model is fixed a priori at M=4. The joint rate function displays markedly non-Gaussian behaviour and some dependence between and . Convergence to a large-deviation principle is mainly reached at τ=15 d, as can be seen from the probability density-based estimates of the joint rate function. The estimates from the Legendre transform are in agreement and already indicate the joint rate function at τ=10 d. The elements of the diffusion matrix are well estimated overall with detailed convergence being somewhat slow in accordance with the univariate analysis for the first FTLE. The estimate of the off-diagonal element D1,2 is particularly good.
The statistical properties of the fluctuations of FTLEs were investigated in a three-level quasi-geostrophic atmospheric model with realistic mean state and variability. The Lyapunov spectrum of the model has almost 100 positive LEs and displays no clear timescale separation.
A principal component analysis of the fluctuations of the FTLEs around their mean values was performed. The scaled covariance matrix of the fluctuations is converged to the limiting diffusion matrix at about τ=15 d. There are substantial correlations among the different FTLEs. The first three empirical orthogonal functions are patterns where the leading positive FTLEs fluctuate together in phase. These modes are largely independent of the integration time τ.
A large-deviation principle can be established for all of the FTLEs. The convergence to the large-deviation limit is slightly slow for the most unstable and the most stable FTLEs and very fast in between. Convergence to the diffusion limit, that is to the Gaussian approximation of the large-deviation regime, is generally faster. Also a joint large-deviation rate function for the first and the second FTLE was successfully estimated beyond the Gaussian approximation. Good correspondence was found between the curvature of the rate functions at the minimum and the corresponding elements of the diffusion matrix.
Two different methods for estimating the large-deviation rate functions from the data were discussed: an approach via the probability density function and an approach using the Legendre transform. The Legendre transform method appears to be generally superior for finding the rate function as (i) convergence occurs at a smaller value of the integration time τ where more independent data are available and (ii) it yields diffusion coefficients fully consistent with their direct estimation from the data. Nevertheless, both methods should be considered side by side as the probability density approach allows one to monitor if/when the probability density function has actually reached the large-deviation regime.
The data and codes relating to this paper are available upon request from the author. They are not publicly accessible, as they were created solely for the purpose of this research study.
The author declares that they have no conflict of interest.
This article is part of the special issue “Numerical modeling, predictability and data assimilation in weather, ocean and climate: A special issue honoring the legacy of Anna Trevisan (1946–2016)”. It is not associated with a conference.
The author would like to thank the three anonymous reviewers for their comments which helped improve the presentation and clarity of the paper.
This paper was edited by Juan Manuel Lopez and reviewed by three anonymous referees.
Benettin, G., Galgani, L., Giorgilli, A., and Strelcyn, J.-M.: Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems: a method for computing all of them, Part 1: Theory, Meccanica, 15, 9–20, 1980.
Billingsley, P.: Probability and Measure, 3rd edn., Wiley, New York, 1995.
Eckmann, J. and Ruelle, D.: Ergodic theory of chaos and strange attractors, Rev. Mod. Phys., 57, 617–656, 1985.
Ehrendorfer, M.: The total energy norm in a quasigeostrophic model, J. Atmos. Sci., 57, 3443–3451, 2000.
Johnson, P. L. and Meneveau, C.: Large-deviation joint statistics of the finite-time Lyapunov spectrum in isotropic turbulence, Phys. Fluids, 27, 085110, https://doi.org/10.1063/1.4928699, 2015.
Kalnay, E.: Atmospheric Modeling, Data Assimilation, and Predictability, Cambridge University Press, Cambridge, 2003.
Kifer, Y.: Large deviations in dynamical systems and stochastic processes, T. Am. Math. Soc., 321, 505–524, 1990.
Kuptsov, P. V. and Parlitz, U.: Theory and computation of covariant Lyapunov vectors, J. Nonlinear Sci., 22, 727–762, 2012.
Kuptsov, P. V. and Politi, A.: Large-deviation approach to space-time chaos, Phys. Rev.Lett., 107, 114101, https://doi.org/10.1103/PhysRevLett.107.114101, 2011.
Kwasniok, F.: Reduced atmospheric models using dynamically motivated basis functions, J. Atmos. Sci., 64, 3452–3474, 2007.
Laffargue, T., Lam, K.-D. N. T., Kurchan, J., and Tailleur, J.: Large deviations of Lyapunov exponents, J. Phys. A-Math. Theor., 46, 254002, https://doi.org/10.1088/1751-8113/46/25/254002, 2013.
Legras, B., and Ghil, M.: Persistent Anomalies, Blocking, and Variations in Atmospheric Predictability, J. Atmos. Sci., 42, 433–471, 1985.
Lorenz, E. N.: Deterministic Nonperiodic Flow, J. Atmos. Sci., 20, 130–141, 1963.
Marshall, J. and Molteni, F.: Toward a dynamical understanding of planetary-scale flow regimes, J. Atmos. Sci., 50, 1792–1818, 1993.
Oseledets, V. I.: A multiplicative ergodic theorem, Characteristic Ljapunov exponents of dynamical systems, Transactions of the Moscow Mathematical Society, 19, 179–210, 1968.
Ott, E.: Chaos in Dynamical Systems, Cambridge University Press, Cambridge, 2002.
Pazó, D., López, J. M., and Politi, A.: Universal scaling of Lyapunov-exponent fluctuations in space-time chaos, Phys. Rev. E, 87, 062909, https://doi.org/10.1103/PhysRevE.87.062909, 2013.
Pikovsky, A. and Politi, A.: Lyapunov Exponents, Cambridge University Press, Cambridge, 2016.
Roads, J. O.: Predictability in the extended range, J. Atmos. Sci., 44, 3495–3527, 1987.
Rohwer, C. M., Angeletti, F., and Touchette, H.: Convergence of large-deviation estimators, Phys. Rev. E, 92, 052104, https://doi.org/10.1103/PhysRevE.92.052104, 2015.
Schubert, S. and Lucarini, V.: Covariant Lyapunov vectors of a quasi-geostrophic baroclinic model: Analysis of instabilities and feedbacks, Q. J. Roy. Meteorol. Soc., 141, 3040–3055, 2015.
Shimada, I. and Nagashima, T.: A Numerical Approach to Ergodic Problem of Dissipative Dynamical Systems, Prog. Theor. Phys., 61, 1605–1616, 1979.
Touchette, H.: The large deviation approach to statistical mechanics, Phys. Rep., 478, 1–69, 2009.
Vannitsem, S.: Predictability of large-scale atmospheric motions: Lyapunov exponents and error dynamics, Chaos, 27, 032101, https://doi.org/10.1063/1.4979042, 2017.
Vannitsem, S. and Lucarini, V.: Statistical and Dynamical Properties of Covariant Lyapunov Vectors in a Coupled Atmosphere-Ocean Model – Multiscale Effects, Geometric Degeneracy, and Error Dynamics, J. Phys. A-Math. Theor., 49, 224001, https://doi.org/10.1088/1751-8113/49/22/224001, 2016.
Vannitsem, S. and Nicolis, C.: Lyapunov Vectors and Error Growth Patterns in a T21L3 Quasigeostrophic Model, J. Atmos. Sci., 54, 347–361, 1997.
Yang, H.-L., Takeuchi, K. A., Ginelli, F., Chaté, H., and Radons, G.: Hyperbolicity and the Effective Dimension of Spatially Extended Dissipative Systems, Phys. Rev. Lett., 102, 074102, https://doi.org/10.1103/PhysRevLett.102.074102, 2009.