the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Numerical bifurcation methods applied to climate models: analysis beyond simulation
Henk A. Dijkstra
In this special issue contribution, I provide a personal view on the role of bifurcation analysis of climate models in the development of a theory of climate system variability. The state of the art of the methodology is shortly outlined, and the main part of the paper deals with examples of what has been done and what has been learned. In addressing these issues, I will discuss the role of a hierarchy of climate models, concentrate on results for spatially extended (stochastic) models (having many degrees of freedom) and evaluate the importance of these results for a theory of climate system variability.
The climate system, comprised of the atmosphere, ocean, cryosphere, land and biosphere components, displays variability on a broad range of temporal and spatial scales. Much information on this variability has become available from observations (both instrumental and proxy) over the last decades. Through these observations, many specific phenomena of variability have been identified, such as the interannual-timescale El Niño–Southern Oscillation (ENSO) in the equatorial Pacific (Philander, 1990) and the millennial-timescale Dansgaard–Oeschger cycles (Clement and Peterson, 2008).
In classical meteorology, the weather is defined as the variability on a timescale of a few days, and climate is the “average weather” where usually an averaging time of 30 years is taken. However, such a concept of climate is not very useful as the climate system displays variability over many timescales. Hence, in modern climate dynamics an often used concept is that of the climate system variability which includes the weather and also variability in the ocean, land, biosphere and ice components. Much of this variability in the climate system is intrinsic (or internal), indicating that it would exist even if the insolation from the Sun were constant. Intrinsic variability arises through instabilities, in most cases associated with positive feedback processes. There is also variability through radiative forcing variations associated with the diurnal and seasonal cycle and variations of the Earth's orbit (Milankovitch forcing). If we do not consider human activities to be part of the climate system, then the changes in atmospheric composition due to anthropogenic emissions are also considered as a forcing. The same can be done with lithospheric processes such that volcanic activity is also a forcing component.
Natural climate variability is then all variability due to natural processes (both intrinsic and forced), and anthropogenic climate change is only that part due to human activities. To reliably project future climate change, a thorough knowledge of the natural variability is required. At the moment, there appear to be two different paradigms of natural climate variability (Fig. 1). One is the classical “background and peaks” framework (Mitchell, 1976), where the peaks are associated with specific phenomena (Ghil, 2002) such as ENSO (Fig. 1a). Another view is that variability constitutes a continuum of fluctuations with scaling behavior; hence “peaks”, apart from the diurnal and annual cycle, are less relevant (Lovejoy and Schertzer, 2013). In this paradigm, several different scaling regimes exist up to multi-millennial timescales, e.g., the weather, macro-weather and climate regimes (Fig. 1b). The “background and peaks” paradigm clearly has a problem with the explanation of the background signal and also regarding the amplitude of the variability on longer than millennial timescales (Lovejoy, 2015). On the other hand, the scaling paradigm needs a better connection to physical processes beyond the weather regime (Franzke et al., 2019). Both paradigms are also limited to temporal variability and do not address spatial patterns associated with the climate system variability.
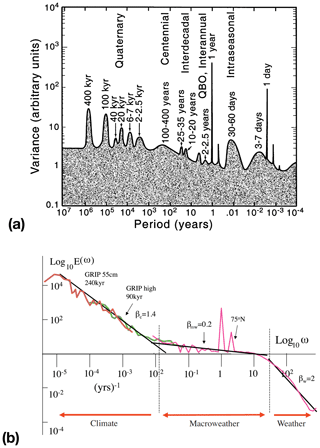
Figure 1(a) The “background and peaks” paradigm as an artist's view of climate system variability (figure slightly modified from Mitchell, 1976; see Ghil, 2002, for details). This figure panel is from Dijkstra and Ghil (2005) and reproduced with permission from AGU. (b) A composite temperature spectrum (figure from Lovejoy et al., 2013; see their Fig. 2 for details) to illustrate the “scaling” paradigm.
To understand the results of the observations, i.e., to relate them to elementary well-established physical principles, the observations themselves are in most cases not enough and models are needed. Fortunately, a hierarchy of such models, from conceptual ones (capturing only a few elementary processes or scales) to global climate models (which are multi-scale and multi-process representations), is available. Traditionally, climate system modeling is seen as an initial value problem. The model equations are integrated in time from a specific initial condition (or an ensemble of them), and then the transient behavior is analyzed. A subsequent statistical analysis is performed on the results using in general uni- or multivariate statistical methods. Often, parameters in the model are varied to study the sensitivity of the results to physical processes (associated with the parameters) and to determine mechanisms of specific phenomena from the statistical analyses.
Changes in parameters can lead to qualitatively different behavior; for example, oscillatory behavior appears or transitions occur. When relatively strong changes occur under small changes of a parameter, critical conditions associated with so-called tipping behavior may have been crossed.
In particular regarding issues of qualitative changes in model behavior once parameters are varied, there is a complementary methodology available from dynamical systems theory, which is targeted to directly compute the asymptotic (long-time) states (attractors) of the model. In the most simple autonomous models (steady forcing), these attractors are fixed points and periodic orbits. Non-autonomous models are studied through pullback attractor analysis (Ghil et al., 2008). Methodology from ergodic theory can be used to study the decay to the attractor of correlations between different observables (Chekroun et al., 2011).
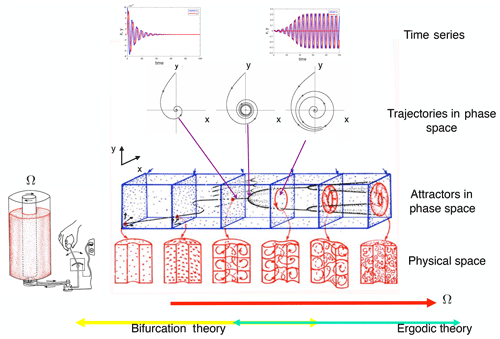
Figure 2Sketch of dynamical systems concepts and approaches for the Taylor–Couette flow (as modified from Abraham and Shaw, 1992). Time series, trajectories and the geometrical view of attractors are sketched. Transition behavior at small values of Ω can be addressed by bifurcation theory; for large values of Ω it can be tackled using ergodic theory.
A canonical problem of transition behavior in fluid dynamics is the flow between two concentric cylinders of which only the inner cylinder rotates with an angular frequency Ω, the Taylor–Couette flow (Koschmieder, 1993). An overview of the regimes of flow behavior and dynamical systems methodology that can be applied is presented in Fig. 2. Here, the rotation rate of the inner cylinder Ω is used as the main parameter which is changed. In the case of small Ω, numerical bifurcation theory can be applied to study the steady states of these models and to determine mechanisms of transition through instabilities. The transient behavior, as shown in time series in Fig. 2, can also be visualized in phase/state space where time is implicit (displaying trajectories). Once Ω is increased, a collective interaction between the different instabilities can lead to variability which cannot be understood as a single bifurcation. Basically, here the realm of complex systems science is entered, which deals with emergent properties due to such collective interactions. For large Ω, eventually a turbulent regime is reached where (actually surprisingly) multiple large-scale statistical steady states can be observed (Huisman et al., 2014).
The main issue addressed in this paper is hence whether such a dynamical systems analysis of models of (parts of) the climate system is useful to understand the variability of this system. In Sect. 2, the model hierarchy is sketched and a short overview will be given of the basic techniques focusing on the application to large-dimensional dynamical systems generated from discretized (stochastic) partial differential equations. In Sect. 3, I will discuss results of studies where dynamical systems analysis has been performed on spatially extended climate models, focusing on what has been done so far and what has been learned. This is followed by Sect. 4, where an outlook is given for the role of dynamical systems analysis in developing an overarching theory of climate variability.
2.1 Model hierarchy
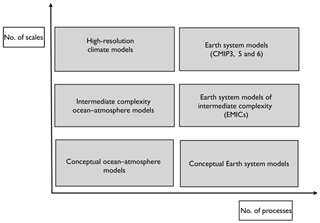
In Dijkstra (2013), I suggested to classify climate models according to the two traits “scales” and “processes” (Fig. 3). Here the trait “scales” refers to both spatial and temporal scales as there exists a relation between both: on smaller spatial scales usually faster processes take place. “Processes” refers to either physical, chemical or biological processes taking place in the different climate subsystems. Models with a limited number of processes and scales are usually referred to as conceptual climate models. Examples are box models of the ocean circulation (Stommel, 1961) and models of glacial–interglacial cycles (Crucifix, 2012), all formulated by small-dimensional systems of ordinary differential equations. Limiting the number of processes, scales can be added by discretizing the governing partial differential equations spatially up to three dimensions. A higher spatial resolution and inclusion of more processes will give models located in the upper right part of the diagram, so-called Earth system models (ESMs). Between the conceptual models and ESMs are so-called intermediate complexity models which are spatially extended (described by partial differential equations) but with fewer scales and/or processes (Fig. 3).
Any spatially extended climate model consists of a set of conservation laws, which are formulated as a set of coupled partial differential equations, that can be written in general form as (Griffies, 2004)
where ℒ and ℳ are linear operators, 𝒩 is a nonlinear operator, u is the state vector, ℱ contains the forcing of the system, and λ indicates the dependence of the operators on parameters. Appropriate boundary and initial conditions have to be added to this set of equations for a well-posed problem.
When Eq. (1) is discretized, eventually a set of differential equations with algebraic constraints arises, which can be written as
where x∈ℝn is the state vector, n its dimension, Mλ is a (often singular) matrix of which every zero row is associated with an algebraic constraint, Lλ is the discretized version of ℒλ, and Fλ and Nλ are the finite-dimensional versions of the forcing and the nonlinear operator, respectively.
When noise is added, the evolution of the flow can generally be described by a stochastic differential-algebraic equation of the form
where Xt is now the stochastic state vector, fλ(Xt) contains the linear and nonlinear processes, and the forcing. The quantity is a vector of nw-independent standard Brownian motions (Gardiner, 2009) and . Here, we use the Itô interpretation to represent unresolved processes but the Stratonovich interpretation can also be used (depending on the nature of processes represented).
2.2 Continuation methods
These methods form part of the numerical bifurcation analysis toolbox; here we are restricted to a single parameter λ. Finding steady states of the system (Eq. 2) versus λ amounts to solving
The idea of pseudo-arc-length continuation (Keller, 1977; Seydel, 1994) is to parametrize branches of solutions with an arc-length parameter s (or an approximation of it, thus the term “pseudo”) and choose s as the continuation parameter. An additional equation is obtained by approximating the normalization condition of the tangent to the branch Γ(s), where the dot refers to the derivative with respect to s, with . More precisely, for a given solution (x0,λ0), the next solution (x,λ) is required to satisfy the constraint
where is the normalized direction vector of the solution family Γ(s) at (x0,λ0) and Δs is an appropriately small step size. Equation (5) stipulates that the projection of onto has the value Δs. Efficient solution methods for high-dimensional systems of the form (Eqs. 4–5) are presented in De Niet et al. (2007) and Thies et al. (2009).
Suppose that the deterministic part of Eq. (3) has a stable fixed point for a given range of parameter values. Then linearization of Eq. (3) around the deterministic steady state yields, with (Kuehn, 2012),
where Aλ(x)≡(Dxfλ)(x) is the Jacobian matrix and Bλ(x)=gλ(x).
In the special case that Mλ is a non-singular matrix, the Eq. (6) can be rewritten (dropping the arguments and subscripts on the matrices) in Itô form as
which represents an n-dimensional Ornstein–Uhlenbeck process. The corresponding stationary covariance matrix C is then determined from the generalized Lyapunov equation:
The Gaussian probability density function at the fixed point can then be computed directly from C. When M is singular, special methods have been devised to cope with the singular part (Baars et al., 2017); also in this case, a generalized Lyapunov equation determines the covariance matrix C. Efficient solution methods for high-dimensional versions of Eq. (8) are presented in Baars et al. (2017).
Numerical bifurcation methodology has been mostly applied to dynamical systems with small n, typically n<10, resulting from conceptual climate models. However, I will focus here solely on results of studies using intermediate complexity models with typically n=104–105, because then also spatial information on the bifurcation behavior is obtained.
From elementary bifurcation theory (Guckenheimer and Holmes, 1990) it is known that only four bifurcations can generically occur when a single parameter is varied: the saddle-node bifurcation, the transcritical bifurcation, the pitchfork bifurcation and the Hopf bifurcation. Because the transcritical bifurcation (solution needed for all values of the parameter) and the pitchfork bifurcation (reflection symmetry needed) require special conditions, the only generic cases are the saddle-node and the Hopf bifurcations. Of these, saddle-node bifurcation only occurs in pairs (because of boundedness of solutions), and hence one often refers to a back-to-back saddle-node bifurcation.
The back-to-back saddle-node bifurcation structure is canonical for tipping points, which we will discuss in Sect. 3.1 below. Although the dynamical system is high-dimensional, the behavior of the system can be dominated by only a few (even only one) positive feedbacks, and hence transitions occur in a low-dimensional space. The Hopf bifurcation is canonical for the occurrence of spontaneous oscillatory behavior associated with one eigenmode of the linearized dynamical system, which is often referred to as the leading mode. A Hopf bifurcation needs the presence of both positive and negative feedbacks; when only a few dominate the dynamical behavior these can be found in high-dimensional systems as discussed in Sect. 3.2. In models where a sequence of Hopf bifurcations occurs, the resulting behavior can in general no longer be described using low-dimensional dynamics. In this case, collective interactions occur and this cannot be captured in a single bifurcation and associated pattern. This case will be discussed in Sect. 3.3 below.
3.1 Tipping points
An overview of possible tipping elements in the Earth's system is given in Lenton et al. (2008) and Steffen et al. (2018) and includes the Arctic winter sea ice, the marine ice sheets (MISs), the Amazon rainforest and the Atlantic Meridional Overturning Circulation (AMOC). Several of the associated transitions are thought to be associated with the existence of a multiple equilibrium regime associated with a back-to-back saddle-node structure, in particular the collapse of the AMOC and that of the MIS.
For a back-to-back saddle-node bifurcation there are two transition scenarios possible, called (i) bifurcation tipping and (ii) noise-induced tipping (Ditlevsen and Johnsen, 2010). In case (i) the parameter crosses a value at one of the saddle-node bifurcations, and in case (ii) a finite amplitude perturbation in the state vector causes a transition (even for a fixed value of the parameter). In the non-autonomous case also rate-induced tipping (Ashwin et al., 2012) is possible. For both cases (i) and (ii), it is crucial to determine the extent of the multiple equilibrium regime (Fig 4): this has been investigated in detail in spatially extended models for the following problems.
-
AMOC. In a substantial number of papers, the bifurcation diagrams for both spatially two- and three-dimensional (intermediate complexity) ocean-only models of the AMOC have been determined (see chap. 6 in Dijkstra, 2005). The most advanced result is for a global ocean model coupled to an energy balance atmospheric model (den Toom et al., 2012), capturing ocean–atmosphere feedbacks, where also a back-to-back saddle-node structure was found.
Numerical bifurcation analyses provided the basis for the stability indicator of the multiple equilibrium regime of the AMOC (Huisman et al., 2010). Here, Mov is the AMOC-induced freshwater transport, and the superscripts n and s indicate the northern and southern boundaries of the Atlantic, respectively. Although the central idea was already formulated in Rahmstorf (1996) and de Vries and Weber (2005), only bifurcation analysis of high-dimensional discretized ocean models provided more rigorous support for the use of this indicator. Although this stability indicator has its problems (Gent, 2018) and needs to be extended in a coupled ocean–atmosphere context, it is often used to investigate the stability of the AMOC (Hawkins et al., 2011).
For a spatially two-dimensional ocean-only model, the covariance matrices C were determined from solving the Lyapunov equation in Eq. (8) in Baars et al. (2017) for the case of noise in the freshwater forcing. While here it served only to test the new Lyapunov equation solver (RAILS), the methodology was extended recently to compute (noise-induced) transition probabilities of the AMOC and to relate that probability to the stability indicator Σ (Castellana et al., 2019). Such transitions are thought to be involved in the Dansgaard–Oeschger (DO) events (Ditlevsen and Johnsen, 2010).
-
MIS. The explicit computation of the bifurcation structure of a spatially one-dimensional marine ice-sheet model (with a moving grounding line) has been carried out only recently (Mulder et al., 2018). Here also a back-to-back saddle-node structure is found, of course compatible with the many initial value problem studies of this model (Schoof, 2007). The gravitational effect of a marine ice sheet on sea level has a stabilizing influence on the ice sheet as seen through a shift in the bifurcation diagram. While this was found in many different model studies (Gomez et al., 2010), the precise mechanism could be deduced from the bifurcation diagram shift (Mulder et al., 2018). For a stochastic MIS model, the covariance matrices C were determined for each stable state in Mulder et al. (2018). Typical noise in the accumulation leads to grounding line variations on the order of 1000 m, while for sea level noise this is about 100 m. In the multiple equilibrium regime, the study of the transition probabilities indicated that, for both noise types, it is more likely to jump from a large ice sheet state to a small ice sheet state than vice versa.
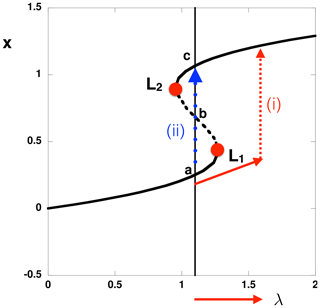
Figure 4The canonical bifurcation diagram with the back-to-back saddle node indicating two stable states (a, c) and an unstable state (b). Bifurcation tipping occurs when the parameter λ crosses the value at L1 or L2. Noise-induced tipping (e.g., from state a to state c) can occur through a perturbation in the state vector (for fixed λ).
In high-dimensional climate models, also so-called edge states or Melancholy states have been computed, for example in a coupled atmospheric sea-ice model investigating ice-covered/ice-free multi-stability (Lucarini and Bódai, 2017). This edge state is a saddle embedded in the boundary between the two basins of attraction of the stable climate states.
3.2 Patterns of sea surface temperature (SST) variability
It is remarkable that on interannual-to-multidecadal timescales the variability in sea surface temperature is organized in large-scale patterns (Fig. 5). These patterns have been detected by using multi-variate analysis on long data sets, such as the HadISST, for example through principal component analysis where the patterns are then contained in the empirical orthogonal functions (EOFs). Well-known and much-studied patterns are those of the El Niño–Southern Oscillation (ENSO), the Atlantic Multidecadal Oscillation (Enfield et al., 2001) and the Pacific Decadal Oscillation (PDO) (Mantua et al., 1997), as shown in Fig. 5.
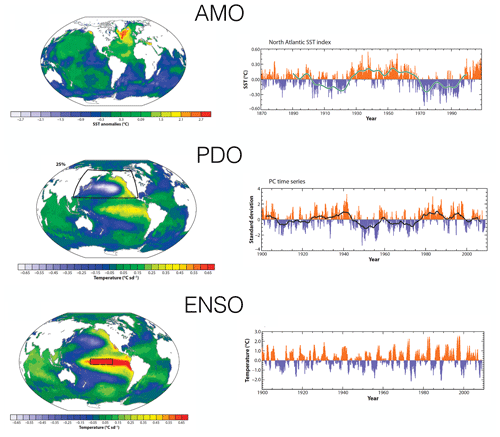
Figure 5Overview of patterns of climate variability (AMO, PDO and ENSO) as determined in Deser et al. (2010) with accompanying time series.
Numerical bifurcation analysis has been applied to several spatially extended models, in particular ENSO, PDO and the AMO.
-
ENSO. The cornerstone intermediate complexity model is the Zebiak–Cane (ZC) model of which the behavior has been extensively analyzed (Zebiak and Cane, 1987). Numerical bifurcation analysis of different versions of the ZC model were performed (see chap. 7 in Dijkstra, 2005), and in each of them a Hopf bifurcation occurs once the coupling strength between the equatorial ocean and atmosphere crosses a critical value. The period of the leading mode is in the interannual range and determined by basin modes, just as in the recharge–discharge oscillator model (Jin, 1997). The spatial pattern of the leading mode is localized into the cold tongue region of the mean (steady) state and shares many similarities with the first EOF from observations.
-
AMO. One of the intermediate complexity models which has been used is a spatially three-dimensional model of the North Atlantic (see chap. 8 in Dijkstra, 2013). The mean (steady) state is generated by a horizontal atmospheric surface buoyancy field which drives a meridional overturning circulation in the ocean model. Numerical bifurcation analysis of this model has shown that the background state destabilizes through a multi-decadal leading mode, and hence a Hopf bifurcation occurs. The timescale of the leading mode can be linked to the basin crossing time of temperature anomalies, and its spatial pattern shares many features with the observed pattern (Kushnir, 1994) when a representation of the continents is considered. The variability can be easily excited through noise in the heat flux, even when the leading mode is decaying in the deterministic case (see chap. 8 in Dijkstra, 2013).
-
PDO. The same bifurcation analysis as for the AMO was applied to a model of two ocean basins which are connected by the Southern Ocean (von der Heydt and Dijkstra, 2007). It was found that the PDO cannot be related to a single mode of variability which arises through a Hopf bifurcation (as for ENSO and the AMO). The key here is that destabilization of the mean (steady) flow can only occur when there is sinking (by the AMOC) in the northern part of the basin. Such sinking is absent in the North Pacific for the present-day climate. Indeed, modern views of the PDO indicate that several different mechanisms are likely important for the existence of PDO variability (Newman et al., 2016).
My interpretation of these results is that several of these SST patterns (but not all) appear through a normal mode which destabilizes the mean state through positive feedbacks; the presence of negative feedbacks causes the oscillatory behavior. In this case, the associated Hopf bifurcation (of a spatially extended model) provides both the dominant timescale of variability and its spatial pattern. The elegant structure of leading modes in ocean models and the ZC model was presented in Dijkstra (2016). The key to why normal modes can be dominant in this variability may be that the nonlinearity in these models is rather weak (it involves advection of heat/salt and not of momentum). Hence the mean state is not modified (rectified) much due to the nonlinear interactions (contrary to the processes shown in the next section).
3.3 Collective interactions and emergent behavior
In the previous two subsections climate system variability phenomena were attributed to low-order dynamics. However, there are many phenomena which are intrinsically caused by the collective interaction of multiple instabilities. Clearly, the role of numerical bifurcation theory becomes quite limited in determining the behavior of these (in general) chaotic dynamical systems; I briefly describe below two examples.
-
Ocean western boundary current variability (WBC). In pure wind-driven barotropic shallow-water models, the bifurcation structure consists of an imperfect pitchfork bifurcation followed by several Hopf bifurcations containing two types of modes: Rossby modes and so-called gyre modes. These gyre modes are eventually responsible for homoclinic orbits which lead to ultra-low-frequency behavior (see chap. 5 in Dijkstra, 2005). When another layer is added, baroclinic instabilities lead to a range of normal modes (Simonnet et al., 2003) which all destabilize. Hence the eventual emergent behavior is induced by their collective interactions. Such behavior can lead to low-frequency behavior in the statistical steady state which has been referred to as the turbulent oscillator (Berloff et al., 2007).
-
Midlatitude atmospheric variability (MAV). Analysis of barotropic spatially extended models of midlatitude atmospheric flows has shown that there are many (highly) unstable equilibria (Legras and Ghil, 1983; Crommelin, 2003). Also here the resulting variability occurs through a collective interaction and low-frequency variability emerges in the statistical equilibrium state (Crommelin et al., 2004). Approaches to understand the dynamics on the attractor have been proposed through transfer operator methods (Tantet et al., 2015).
The cases briefly described above are examples of strongly nonlinear systems, where the nonlinearities occur in the momentum advection and where the mean state is strongly modified through rectification. Of course, there are many more examples of such geophysical systems, in particular on timescales up to interannual both in the ocean (internal waves) and the atmosphere (weather).
In this paper, I have given a short overview of results of studies where continuation methods were applied to spatially extended climate models. My interpretation of these results is that there are climate variability phenomena that can be attributed to low-order behavior; only one or a few spatial patterns are involved, associated with dominant feedbacks. Several of these studies have shown that successive instability behavior can also occur. This leads to a collective interaction between patterns that is eventually responsible for emergent variability in climate models. A summary of the different phenomena based on this distinction is provided in Fig. 6, with low-order phenomena (ENSO, AMO), emergent phenomena due to collective interactions (WBC, MAV) and tipping behavior (AMOC/DO, MIS). With this information, I now come back to the two paradigms of climate variability, as mentioned in the introduction.
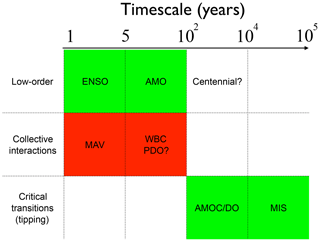
Figure 6Summary of what has been learned from dynamical systems analysis of spatially extended climate models, based on the distinction of low-order phenomena, emergent phenomena through collective interactions and critical transitions. The “hope” is that mechanisms of the phenomena in the green boxes can be determined from numerical bifurcation analysis of intermediate complexity climate models.
This first challenge I see is to better understand processes behind the background variability which is “red noise like” in Mitchell (1976) and encompasses different regimes in Lovejoy et al. (2013). Franzke et al. (2019) describe the different ways (multifractal cascading processes, state-dependent noise, etc.) of how scaling behavior can appear in time series. To connect scaling behavior to clear physical processes, one idea would be to identify at each timescale range the “slow” passive component in the climate system and the “fast” forcing it receives. For example, for SST variability the Hasselmann (1976) model of an ocean mixed layer forced with a rapidly fluctuating atmospheric heat flux identifies such components, leading to a red noise background. However, when another variable is considered, such as sea surface height, then the background model is an ocean thermocline layer forced with noisy wind-stress forcing, leading to a correlated additive–multiplicative (CAM) noise model (Sardeshmukh and Sura, 2009; Castellana et al., 2018). In the “climate regime” of Lovejoy et al. (2013), an appropriate model could be a marine ice sheet forced with rapidly fluctuating accumulation noise or sea level noise (Mulder et al., 2018), also leading to CAM noise. This would give power law spectral behavior (in the proxy record), being indeed very different from the picture of Mitchell (1976). The slope changes of the different regimes as in Lovejoy et al. (2013) could then maybe be related to a change in slow component in the climate system determining this background signal.
Once the physics of this background are clear, the next challenge is to attribute spatial patterns which rise above it to specific instabilities. Several spatial patterns of SST variability are robust over the model hierarchy. I would interpret this to indicate that these spatial patterns, such as ENSO and the AMO, are due to a single-mode destabilization of the background induced by dominant large-scale feedbacks. These spatial patterns can already be captured in detail in intermediate complexity models, such as the ZC model for ENSO. Capturing the temporal variability involves representation of small-scale processes (noise) and possibly non-normal growth (Penland and Sardeshmukh, 1995; Farrell and Ioannou, 1996; Tziperman et al., 2008), and one may need more detailed models than intermediate complexity models. Another case where a low-order explanation may be appropriate is centennial variability. The timescale here arises by buoyancy anomalies which propagate over the AMOC loop (also called overturning modes and loop oscillations). These can be excited in this model by applying noise, e.g., in the freshwater flux or in the heat flux (Dijkstra and von der Heydt, 2017).
Other spatial patterns (such as the MAV and WBC variability) arise through a collective interaction of instabilities and hence can only be captured in detail through models high in the hierarchy (representing a multitude of scales). This holds for example for the path variability of the Kuroshio Current, where it is known that the interactions of the barotropic instabilities of the current and the (baroclinic) mesoscale eddy field are important (Qiu and Chen, 2005). Such collective interactions may eventually also be needed to explain the PDO. Furthermore, analysis of high-resolution (near-eddy resolving) ocean model has indicated that a new type of multidecadal variability emerges through a collective interaction, the Southern Ocean mode. A Lorenz type energy analysis has indicated (Jüling et al., 2019) that eddy–mean-flow interaction is crucial for the existence of this type of variability. Also in this case, there is no single (normal) mode of variability which determines the dominant time and spatial pattern.
Apart from the internal variability introduced by single normal (oscillatory) modes and collective phenomena, also clear large-scale tipping phenomena (in the sense of critical transitions) can affect climate variability. The canonical behavior is a back-to-back saddle-node bifurcation appearing generically in conceptual models. It was shown here that for models of the AMOC and MIS, indeed such bifurcation behavior is found in high-dimensional models. Transition behavior hence may occur when critical conditions are crossed or through noise in the multiple equilibrium regime. A third challenge I see is to show that such transitions remain robust once small-scale processes are included; work in this direction has been initiated (Lucarini and Bódai, 2017).
All of the results of continuation methods described above were obtained under stationary forcing and this seems disjoint from the real climate system, which is obviously forced by a non-stationary insolation component (on diurnal, seasonal and orbital timescales). For the present-day climate system, there is also the non-stationary anthropogenic component of climate change. A fourth challenge is to understand the relevance of these diurnal and seasonal non-stationary periodic components in natural internal variability on longer timescales. While one may argue that they are irrelevant and are averaged out, few detailed results are available. Probably only on interannual timescales can there be an interaction between the seasonal cycle and internal variability, for example, with the ENSO mode (due to nonlinear resonances). On very large timescales, however, certainly the non-stationary orbital forcing is crucial for the observed variability such as glacial cycles. The modification of natural variability under climate forcing is of course also a challenging issue.
Has the end point been reached of the models for which bifurcation analysis can be applied? Since starting with this endeavor in the early 1990s, I have been repeatedly asked this question. When we showed results for spatially two-dimensional ocean models, we were asked if we could do this for three-dimensional models. When we did, the question was on the application to ocean–atmosphere models. Although there are certainly still interesting details to be investigated in the ocean-only context, I think the main challenge with these models is to develop theory for internal variability in the geological past (Zachos et al., 2001). In the last few years my group has turned to develop techniques to incorporate sea ice and land ice and to be able to change the geometry of the ocean basin during the continuation (Mulder et al., 2017). With a carbon cycle model still to be implemented, I think that the resulting methodology will be suited to tackle what processes determined the background states in the past and which variability can possibly be attributed to low-order dynamics. It will also be possible to investigate explicit bifurcation behavior arising from carbon-cycle feedbacks.
The author declares that there is no conflict of interest.
This article is part of the special issue “Centennial issue on nonlinear geophysics: accomplishments of the past, challenges of the future”. It is not associated with a conference.
The author thanks his “partner in crime”, Fred W. Wubs (University of Groningen, the Netherlands), for the (now ∼25 years) long and very fruitful (still very active) collaboration regarding the application of numerical bifurcation analysis in high-dimensional stochastic dynamical systems arising from climate models. I also thank the many contributions from the PhDs and postdocs who have worked on our joint projects, in particular the current ones: Erik Mulder, Sven Baars and Daniele Castellana. I also thank Andrew Keane and Bernd Krauskopf (University of Auckland, NZ) for organizing a session at the SIAM conference on Dynamical Systems (May 2019), where the ideas in this paper could be presented.
This work was sponsored by the Netherlands Earth System Science Centre (NESSC), financially supported by the Ministry of Education, Culture and Science (OCW (grant no. 024.002.001)).
This paper was edited by Ana M. Mancho and reviewed by two anonymous referees.
Abraham, R. and Shaw, C.: Dynamics: The Geometry of Behavior, Addison-Wesley, Redwood City, California, USA, 1992. a
Ashwin, P., Wieczorek, S., Vitolo, R., and Cox, P.: Tipping points in open systems: bifurcation, noise-induced and rate-dependent examples in the climate system, Philos. T. Roy. Soc. A, 370, 1166–1184, 2012. a
Baars, S., Viebahn, J. P., Mulder, T. E., Kuehn, C., Wubs, F. W., and Dijkstra, H. A.: Continuation of probability density functions using a generalized Lyapunov approach, J. Comput. Phys., 336, 627–643, 2017. a, b, c
Berloff, P. S., Hogg, A. M., and Dewar, W. K.: The turbulent oscillator: a mechanism of low-frequency variability of the wind-driven ocean gyres, J. Phys. Oceanogr., 37, 2362–2386, 2007. a
Castellana, D., Wubs, F., and Dijkstra, H.: A statistical significance test for sea-level variability, Dynamics and Statistics of the Climate System, 3, dzy008, https://doi.org/10.1093/climsys/dzy008, 2018. a
Castellana, D., Baars, S., Wubs, F., and Dijkstra, H.: Transition Probabilities of Noise-induced AMOC Transitions, Nature Scientific Reports, submitted, 2019. a
Chekroun, M. D., Simonnet, E., and Ghil, M.: Stochastic climate dynamics: Random attractors and time-dependent invariant measures, Physica D, 240, 1685–1700, 2011. a
Clement, A. C. and Peterson, L. C.: Mechanisms of abrupt climate change of the last glacial period, Rev. Geophys., 46, RG4002, https://doi.org/10.1029/2006RG000204., 2008. a
Crommelin, D.: Regime transitions and heteroclinic connections in a barotropic atmosphere, J. Atmos. Sci., 60, 229–246, 2003. a
Crommelin, D., Opsteegh, J., and Verhulst, F.: A mechanism for atmospheric regime behavior, J. Atmos. Sci., 61, 1406–1419, 2004. a
Crucifix, M.: Oscillators and relaxation phenomena in Pleistocene climate theory, Philos. T. Roy. Soc. A, 370, 1140–1165, 2012. a
De Niet, A. C., Wubs, F., Terwisscha van Scheltinga, A. D., and Dijkstra, H. A.: A tailored preconditioner for high-resolution implicit ocean models, J. Comput. Phys., 277, 654–679, 2007. a
den Toom, M. d., Dijkstra, H. A., Cimatoribus, A. A., and Drijfhout, S. S.: Effect of Atmospheric Feedbacks on the Stability of the Atlantic Meridional Overturning Circulation, J. Climate, 25, 4081–4096, 2012. a
Deser, C., Alexander, M. a., Xie, S.-P., and Phillips, A. S.: Sea Surface Temperature Variability: Patterns and Mechanisms, Annu. Rev. Mar. Sci., 2, 115–143, 2010. a
de Vries, P. and Weber, S. L.: The Atlantic freshwater budget as a diagnostic for the existence of a stable shut down of the meridional overturning circulation, Geophys. Res. Lett., 32, L09606, https://doi.org/10.1029/2004GL021450, 2005. a
Dijkstra, H.: A Normal Mode Perspective of Intrinsic Ocean-Climate Variability, Annu. Rev. Fluid Mech., 48, 341–363, 2016. a
Dijkstra, H. A.: Nonlinear Physical Oceanography: A Dynamical Systems Approach to the Large Scale Ocean Circulation and El Niño, 2nd revised and enlarged edn., Springer, New York, 532 pp., 2005. a, b, c
Dijkstra, H. A.: Nonlinear Climate Dynamics, Cambridge University Press, Cambridge, UK, 2013. a, b, c, d
Dijkstra, H. A. and Ghil, M.: Low-frequency variability of the large-scale ocean circulation: A dynamical systems approach, Rev. Geophys., 43, RG3002, https://doi.org/10.1029/2002RG000122, 2005. a
Dijkstra, H. A. and von der Heydt, A. S.: Basic mechanisms of centennial climate variability, Past Global Changes Magazine, 25, 150–151, 2017. a
Ditlevsen, P. D. and Johnsen, S. J.: Tipping points: Early warning and wishful thinking, Geophys. Res. Lett., 37, L19703, https://doi.org/10.1029/2010GL044486, 2010. a, b
Enfield, D. B., Mestas-Nunes, A. M., and Trimble, P.: The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental US, Geophys. Res. Lett., 28, 2077–2080, 2001. a
Farrell, B. F. and Ioannou, P. J.: Generalized stability theory: Part I: Autnomous operators, J. Atmos. Sci., 53, 2025–2040, 1996. a
Franzke, C. L. E., Barbosa, S., Blender, R., Fredriksen, H., Laepple, T., Lambert, F., Nilsen, T., Rypdal T., Rypdal, M., Scotto, M., Vannitsem, S., Watkins, N., Yang, L., and Yuan, N.: The Structure of Climate Variability Across Scales, Rev. Geophys., submitted, 2019. a, b
Gardiner, C.: Stochastic Methods: A Handbook for the Natural and Social Sciences, Springer, New York, 2009. a
Gent, P. R.: A commentary on the Atlantic meridional overturning circulation stability in climate models, Ocean Model., 122, 57–66, https://doi.org/10.1016/j.ocemod.2017.12.006, 2018. a
Ghil, M.: Natural Climate Variability, in: Encyclopedia of Global Environmental Change, volume 1, edited by: Munn, T., MacCracken, M. C., and Perry, J. S., Wiley, Hoboken, New Jersey, 2002. a, b
Ghil, M., Chekroun, M., and Simonnet, E.: Climate dynamics and fluid mechanics: Natural variability and related uncertainties, Physica D, 237, 2111–2126, 2008. a
Gomez, N., Mitrovica, J. X., Huybers, P., and Clark, P. U.: Sea level as a stabilizing factor for marine-ice-sheet grounding lines, Nat. Geosci., 3, 850–853, 2010. a
Griffies, S. M.: Fundamentals of ocean-climate models, Princeton University Press, Princeton, USA, 2004. a
Guckenheimer, J. and Holmes, P.: Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields, 2e edn., Springer-Verlag, Berlin/Heidelberg, 1990. a
Hasselmann, K.: Stochastic climate models. I: Theory, Tellus, 28, 473–485, 1976. a
Hawkins, E., Smith, R. S., Allison, L. C., Gregory, J. M., Woollings, T. J., Pohlmann, H., and De Cuevas, B.: Bistability of the Atlantic overturning circulation in a global climate model and links to ocean freshwater transport, Geophys. Res. Lett., 38, L10605, https://doi.org/10.1029/2011GL047208, 2011. a
Huisman, S. E., den Toom, M., Dijkstra, H. A., and Drijfhout, S.: An Indicator of the Multiple Equilibria Regime of the Atlantic Meridional Overturning Circulation, J. Phys. Oceanogr., 40, 551–567, 2010. a
Huisman, S. G., van der Veen, R. C. A., Sun, C., and Lohse, D.: Multiple states in highly turbulent Taylor-Couette flow, Nat. Commun., 5, 3820, https://doi.org/10.1038/ncomms4820, 2014. a
Jin, F.-F.: An equatorial recharge paradigm for ENSO. I: Conceptual Model, J. Atmos. Sci., 54, 811–829, 1997. a
Jüling, A., Viebahn, J. P., Drijfhout, S. S., and Dijkstra, H. A.: Energetics of the Southern Ocean Mode, J. Geophys. Res.-Oceans, 123, 9283–9304, 2019. a
Keller, H. B.: Numerical solution of bifurcation and nonlinear eigenvalue problems, in: Applications of Bifurcation Theory, edited by: Rabinowitz, P. H., Academic Press, New York, USA, 1977. a
Koschmieder, E. L.: Bénard Cells and Taylor Vortices, Cambridge University Press, Cambridge, UK, 1993. a
Kuehn, C.: Deterministic continuation of stochastic metastable equilibria via Lyapunov equations and ellipsoids, SIAM J. Sci. Comput., 34, A1635–A1658, 2012. a
Kushnir, Y.: Interdecadal variations in North Atlantic sea surface temperature and associated atmospheric conditions, J. Phys. Oceanogr., 7, 141–157, 1994. a
Legras, B. and Ghil, M.: Ecoulements atmosphériques stationnaires, périodiques et apériodiques, in: Two-Dimensional Turbulence, edited by: Moreau, R., Gauthier-Villars, Paris, J. Méc. Théor. Appl., 45–82, 1983. a
Lenton, T. M., Held, H., Kriegler, E., Hall, J. W., Lucht, W., Rahmstorf, S., and Schellnhuber, H. J.: Tipping elements in the Earth's climate system, P. Natl. Acad. Sci. USA, 105, 1786–93, 2008. a
Lovejoy, S.: A voyage through scales, a missing quadrillion and why the climate is not what you expect, Clim. Dynam., 44, 3187–3210, 2015. a
Lovejoy, S. and Schertzer, D.: The weather and climate: emergent laws and multifractal cascades, Cambridge University Press, First Cambridge Mathematical Library Edition, Cambridge, UK, 2013. a
Lovejoy, S., Schertzer, D., and Varon, D.: Do GCMs predict the climate ... or macroweather?, Earth Syst. Dynam., 4, 439–454, https://doi.org/10.5194/esd-4-439-2013, 2013. a, b, c, d
Lucarini, V. and Bódai, T.: Edge states in the climate system: exploring global instabilities and critical transitions, Nonlinearity, 30, R32, https://doi.org/10.1088/1361-6544/aa6b11, 2017. a, b
Mantua, N. J., Hare, S., Zhang, Y., Wallace, J. M., and Francis, R. C.: A Pacific interdecadal climate oscillation with impacts on salmon production, B. Am. Meteor. Soc., 78, 1069–1079, 1997. a
Mitchell, J. M.: An overview of climate variability and its causal mechanisms, Quaternary Res., 6, 481–493, 1976. a, b, c, d
Mulder, T. E., Baatsen, M. L. J., Wubs, F. W., and Dijkstra, H. A.: Efficient computation of past global ocean circulation patterns using continuation in paleobathymetry, Ocean Model., 115, 77–85, 2017. a
Mulder, T. E., Baars, S., Wubs, F. W., and Dijkstra, H. A.: Stochastic marine ice sheet variability, J. Fluid Mech., 843, 748–777, 2018. a, b, c, d
Newman, M., Alexander, M. A., Ault, T. R., Cobb, K. M., Deser, C., Di Lorenzo, E., Mantua, N. J., Miller, A. J., Minobe, S., Nakamura, H., Schneider, N., Vimont, D. J., Phillips, A. S., Scott, J. D., and Smith, C. A.: The Pacific Decadal Oscillation, Revisited, J. Climate, 29, 4399–4427, 2016. a
Penland, C. and Sardeshmukh, P. D.: The optimal growth of tropical sea surface temperature anomalies, J. Climate, 8, 1999–2024, 1995. a
Philander, S. G. H.: El Niño and the Southern Oscillation, Academic Press, New York, 1990. a
Qiu, B. and Chen, S.: Variability of the Kuroshio Extension Jet, Recirculation Gyre and Mesocale Eddies on decadal time scales, J. Phys. Oceanogr., 35, 2090–2103, 2005. a
Rahmstorf, S.: On the freshwater forcing and transport of the Atlantic thermohaline circulation, Clim. Dynam., 12, 799–811, 1996. a
Sardeshmukh, P. D. and Sura, P.: Reconciling Non-Gaussian Climate Statistics with Linear Dynamics, J. Climate, 22, 1193–1207, 2009. a
Schoof, C.: Ice sheet grounding line dynamics: Steady states, stability, and hysteresis, J. Geophys. Res., 112, F03S28, https://doi.org/10.1029/2006JF000664, 2007. a
Seydel, R.: Practical Bifurcation and Stability Analysis: From Equilibrium to Chaos, Springer-Verlag, New York, USA, 1994. a
Simonnet, E., Ghil, M., Ide, K., Temam, R., and Wang, S.: Low-frequency variability in shallow-water models of the wind-driven ocean circulation. Part I: Steady-state solutions, J. Phys. Oceanogr., 33, 712–728, 2003. a
Steffen, W., Rockström, J., Richardson, K., Lenton, T. M., Folke, C., Liverman, D., Summerhayes, C. P., Barnosky, A. D., Cornell, S. E., Crucifix, M., Donges, J. F., Fetzer, I., Lade, S. J., Scheffer, M., Winkelmann, R., and Schellnhuber, H. J.: Trajectories of the Earth System in the Anthropocene, P. Natl. Acad. Sci. USA, 115, 8252–8259, 2018. a
Stommel, H.: Thermohaline convection with two stable regimes of flow, Tellus, 2, 244–230, 1961. a
Tantet, A., van der Burgt, F. R., and Dijkstra, H. A.: An early warning indicator for atmospheric blocking events using transfer operators, Chaos: An Interdisciplinary Journal of Nonlinear Science, 25, 036406, https://doi.org/10.1063/1.4908174, 2015. a
Thies, J., Wubs, F., and Dijkstra, H. A.: Bifurcation analysis of 3D ocean flows using a parallel fully-implicit ocean model, Ocean Model., 30, 287–297, 2009. a
Tziperman, E., Zanna, L., and Penland, C.: Nonnormal Thermohaline Circulation Dynamics in a Coupled Ocean–Atmosphere GCM, J. Phys. Oceanogr., 38, 588–604, 2008. a
von der Heydt, A. and Dijkstra, H. A.: Localization of multidecadal variability: I. Cross equatorial transport and interbasin exchange, J. Phys. Oceanogr., 37, 2401–2414, 2007. a
Zachos, J., Pagani, M., Sloan, L., Thomas, E., and Billups, K.: Trends, Rhythms, and Aberrations in Global Climate 65 Ma to Present, Science, 292, 686–693, 2001. a
Zebiak, S. E. and Cane, M. A.: A model El Niño-Southern Oscillation, Mon. Weather Rev., 115, 2262–2278, 1987. a





