the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Compacting the description of a time-dependent multivariable system and its multivariable driver by reducing the state vectors to aggregate scalars: the Earth's solar-wind-driven magnetosphere
Joseph E. Borovsky
Adnane Osmane
Using the solar-wind-driven magnetosphere–ionosphere–thermosphere system, a methodology is developed to reduce a state-vector description of a time-dependent driven system to a composite scalar picture of the activity in the system. The technique uses canonical correlation analysis to reduce the time-dependent system and driver state vectors to time-dependent system and driver scalars, with the scalars describing the response in the system that is most-closely related to the driver. This reduced description has advantages: low noise, high prediction efficiency, linearity in the described system response to the driver, and compactness. The methodology identifies independent modes of reaction of a system to its driver. The analysis of the magnetospheric system is demonstrated. Using autocorrelation analysis, Jensen–Shannon complexity analysis, and permutation-entropy analysis the properties of the derived aggregate scalars are assessed and a new mode of reaction of the magnetosphere to the solar wind is found. This state-vector-reduction technique may be useful for other multivariable systems driven by multiple inputs.
In this report a methodology is described that can produce a compact description of the behavior of a time-dependent, multivariable system driven by a time-dependent, multivariable driver or by multiple drivers. The system used to develop this methodology is the Earth's magnetosphere–ionosphere–thermosphere system driven by the time-dependent solar wind. The spatial domain wherein the Earth's magnetic field dominates over the solar wind is known as the magnetosphere. The interaction between the solar wind, and the magnetosphere is surprisingly complex and the magnetosphere's evolution in response to the time-varying solar wind is rich and diverse. The magnetospheric system is characterized by multiple subsystems that interact with each other (cf. Lyon, 2000; Otto, 2005; Siscoe, 2011; Eastwood et al., 2015; Borovsky and Valdivia, 2018): almost 6 orders of magnitude of spatial scales are involved in the global behavior of the magnetosphere, from ∼1 to km. This system is highly coupled, dynamic, with memory and with feedback loops. Multiple physical processes act to couple the various subsystems, with the strength of the couplings evolving with time as the subsystems evolve owing to the couplings. Even after a half of a century of measurements and analysis, its subsystems and the couplings between its subsystems are not fully understood (Stern, 1989, 1996; Denton et al., 2016). It has been argued that the system adjectives “adaptive”, “nonlinear”, “dissipative”, and “complex” apply to the magnetospheric system (Borovsky and Valdivia, 2018). (See also the earlier systems analyses by Horton et al., 1999, Chapman et al., 2004, Valdivia et al., 2005, 2013, and Sharma, 2010.) The magnetospheric system is well measured: there are hundreds of thousands of hours of simultaneous measurements of various aspects of the magnetospheric system and its solar-wind driver over the five decades of the “space age” (cf. Stern, 1989, 1996; King and Papitashvili, 2005).
The methodology developed here creates a compact description of a time-dependent, multivariable system driven by a time-dependent, multivariable driver. The diverse variables describing the system may be intercorrelated, and the variables describing the driving may be intercorrelated. The methodology was developed to gain an understanding of the Earth's magnetosphere–ionosphere–thermosphere system as driven by the solar wind. To utilize the methodology the system and its driver are conceptualized by a time-dependent, multidimensional system state vector S(t) and a time-dependent, multidimensional driver state vector D(t), with the assumption that the driver vector D affects the system vector S, but not vice versa, written D→S. The individual time-dependent scalar variables making up the state vector S(t) are time-dependent measures of various forms of activity in the system and various properties of the system, and the individual time-dependent scalar variables making up the driver state vector D(t) are various time-dependent measures of the properties of the drivers of the system. We will utilize the correlation properties between the components (individual time-dependent variables) of S and the components of D. Canonical correlation analysis (CCA) will be used to derive scalar projections (dot products) of S(t) and scalar projections of D(t) that have the highest Pearson linear correlation coefficient between them. The derived scalar projections S(1)(t), S(2)(t), S(3)(t), … of the vector S(t) will be composite (aggregate) measures of activity in the system, and the derived scalar projections D(1)(t), D(2)(t), D(3)(t), … of the vector D(t) will be the composite drivers of S(1)(t), S(2)(t), S(3)(t), …, respectively. In essence, the aggregate variables S(1)(t), S(2)(t), S(3)(t), … are “latent variables” of the system constructed from the “manifest variables” in the system state vector. This reduced scalar picture D(i)→S(i) of the system driven by the driver focuses on the time-dependent properties of the system that react to the driver. By maximizing the correlations, the predictability of the system from knowledge of the state of the driver is also maximized.
The solar-wind-driven magnetospheric system very cleanly follows the D→S picture where the driver affects the system, but the system does not affect the driver. The Earth's magnetosphere has no influence whatsoever on the properties of the solar wind that passes the Earth. Measurements of this magnetospheric system will be used in Sects. 2 and 3 to explore the mathematical reduction of the state-vector D(t)→S(t) picture to the composite-scalar D(i)(t)→S(i)(t) picture. Table 1 lists the nine time-dependent measurements of the magnetosphere in the system state vector S and the eight time-dependent measurements of the solar wind in the driver state vector D. The individual variables in the system state vector and in the driver state vector are described in the Appendix.
Table 1The nine time-dependent variables going into the system state vector S(t) of the magnetosphere and the eight time-dependent variables going into the driver state vector D(t) of the solar wind.

This report is organized as follows. In Sect. 2 the CCA approach is applied to the magnetospheric system driven by the solar wind to derive the first three time-dependent sets of composite variables S(1)(t) and D(1)(t), S(2)(t) and D(2)(t), and S(3)(t) and D(3)(t) from the state vectors S(t) and D(t). In Sect. 3 the three sets of composite variables S(i) and D(i) for the magnetospheric system are explored, and the complexity–entropy properties of the aggregate variable S(1)(t) are analyzed. In Sect. 4 the advantages of the reduced D(i)→S(i) scalar description are examined: these advantages include (a) a compact description of global system-wide reactions to variations in the driver, (b) increased predictability of the system from knowledge of the driver, (c) linearity in the description of the system's response to the driver, and (d) lower noise in correlations between the system variables and the driver variables. The reduced scalar picture can also reveal independent modes of reaction of the system to the driver, providing insight into the behavior of the system in reaction to complexities in the driver. The variables of the magnetospheric and solar-wind state vectors are described in the Appendix.
Using the Earth's magnetosphere–ionosphere–thermosphere system as driven by the solar wind, the reduction of a time-dependent state-vector picture D(t)→S(t) to the time-dependent composite-variable-pair picture D(i)(t)→S(i)(t) will be performed. The nine measured variables chosen for the nine-dimensional magnetospheric system state vector S appear in the first column of Table 1, and the eight measured variables chosen for the eight-dimensional solar-wind driver state vector D appear in the second column of Table 1, with explanations of those measures deferred to the Appendix.
One-hour averages of all magnetospheric and solar-wind variables are used in the years 1991–2007. No time lags are used between the solar-wind measurements and the magnetospheric measurements: most expected time lags will be about 1 h (e.g., Clauer et al., 1981; Smith et al., 1999), which is the time resolution of the data set.
Canonical correlation analysis (CCA) is applied to the time-dependent state vectors S(t) and D(t). CCA finds correlation patterns between two multivariable data sets (Nimon et al., 2010; Hair et al., 2010). It yields pairs of composite (aggregate) variables (a) that are linear combinations of the variables of the two data sets and (b) that have maximal correlations with each other. Each pair of composite variables is called the “Nth canonical correlation”. From the data sets of S(t) and D(t) the first pair of composite variables yielded (the first canonical variates) is S(1)(t) and D(1)(t): these two variables are projections of S and D given by and , where CS1 and CD1 are time-independent coefficient (weight) vectors. S(1) and D(1) are the composite variables from S and D that have the highest Pearson linear correlation coefficient with each other. Here, CCA is in a sense creating the system function S(1)(t) that is most reactive to the driver vector D(t) and creating the driver scalar function D(1)(t) that describes that driving. CCA then yields other pairs of composite variables S(2) and D(2) (the second canonical correlation), S(3) and D(3) (the third canonical correlation), etc. S(2) and D(2) are the projections of S and D that have the highest correlation with each other, provided that S(2) and D(2) are uncorrelated with S(1) and D(1). S(3) and D(3) are the projections of S and D that have the highest correlations with each other, provided they are uncorrelated with S(1), S(2), D(1), and D(2). S(1)(t), S(2)(t), and S(3)(t) represent three independent modes of reaction of the global system to the driver D(t). The CCA process will identify these modes (and their respective drivers).
CCA is a matrix equation solution, non-iterative, that yields a single unique solution (Johnson and Wichern, 2007). CCA operates on standardized variables (with the mean value subtracted and the values then divided by the standard deviation), denoted with an asterisk. (For each variable the mean value and standard deviation are calculated for the entire data set.) CCA operates most efficiently on variables that are Gaussian distributed: hence the logarithms of some variables are used to yield more-Gaussian-like distributions. All standardized variables v* have a mean value of zero, a standard deviation unity, and no units.
When CCA is applied to the 1991–2007 S(t) and D(t) data sets (see Table 1), the first canonical pair of time-dependent variables is
S(1) and D(1) have mean values of zero and standard deviations of unity. The derived composite variables given by expressions (1) are robust and reproducible: applying the CCA process to various subsets of the full 1991–2007 data set, the CCA process repeatedly yields essentially the same coefficients that are in Eqs. (1a) and (1b) (cf. Borovsky and Denton, 2018).
CCA applied to the time-dependent state vectors S(t) and D(t) for the 1991–2007 data set yields the second canonical pair of time-dependent scalar variables as
For the 1991–2007 data set CCA yields the third canonical pair of time-dependent scalar variables as
The properties of S(1)(t) and D(1)(t), S(2)(t) and D(2)(t), and S(3)(t) and D(3)(t) as given by Eqs. (1)–(3) are explored in Sect. 3.
The three sets of composite variables S(1) and D(1), S(2) and D(2), and S(3) and D(3) for the magnetospheric system are explored and the advantages of the reduced D(i)→S(i) scalar description are investigated.
3.1 The primary mode of system response as represented by D(1)→S(1)
In Fig. 1 the composite system variable S(1) (as given by Eq. 1a) is plotted for the years 1991–2007 as a function of the composite driver variable D(1) (as given by Eq. 1b). Each black point in Fig. 1 represents 1 h of data. The Pearson linear correlation coefficient between S(1) and D(1) for the 1991–2007 data set is rcorr=0.921. Accordingly, % of the variance of the system function S(1)(t) is described by the driver function D(1)(t), and so 15.2 % of the variance of S(1) is unaccounted for by D(1). The blue line in Fig. 1 is a linear-regression fit to S(1), and the red curve is a 50-point vertical running average of the black points. Note the approximate linearity of system variable S(1) as a function of driver variable D(1), indicated by the manner in which the running average tracks the linear-regression line.
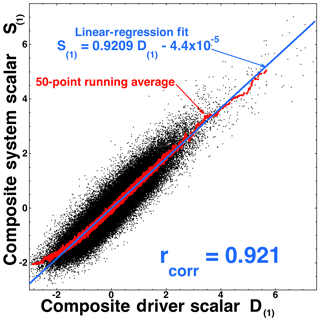
Figure 1The aggregate system scalar S(1) is plotted as a function of the driver scalar D(1) for the 1 h resolution 1991–2007 data set. Each black point is 1 h of data.
Note that whereas the correlation coefficient between S(1)(t) and D(1)(t) is rcorr=0.921, the maximum correlation coefficient between any single variable in the system state vector S(t) and any single variable in the driver state vector D(t) is only rcorr=0.586 (between and .
As a further note, the Pearson linear correlation coefficients between S(1) and various “physics-based” solar-wind driver functions from the literature are the following: +0.378 for −vswBz, +0.557 for vswBsouth (Eq. 2 of Holzer and Slavin, 1979), +0.679 for the Newell function dΦ∕dt (Eq. 1 of Newell et al., 2007), +0.723 for the quick reconnection function Rq (Eq. 8 of Borovsky and Birn, 2014), and +0.761 for the nonlinear reconnection-coupled MHD generator with Bohm viscosity (Eq. 65 of Borovsky, 2013). All of these driver functions have poor correlations with S(1) in comparison with the +0.921 correlation of D(1) with S(1).
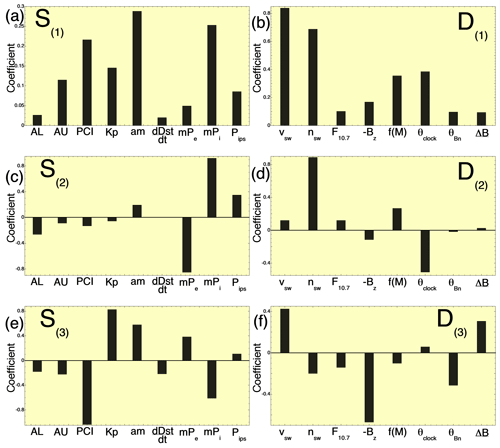
Figure 2Plots of the nine components of the coefficient vectors used to project the system state vector S into the aggregate variables S(1) (a), S(2) (c), and S(3) (e) and plots of the eight components of the coefficient vectors used to project the driver state vector D into the driver scalar variables D(1) (b), D(2) (d), and D(3) (f).
In the six panels of Fig. 2 the coefficients of the six vectors CS1, CD1, CS2, CD2, CS3, and CD3 are plotted. (These are the coefficients in Eqs. 1–3.) Examining these six panels enables the reaction modes represented by S(1), S(2), and S(3) to be interpreted as well as their drivers D(1), D(2), and D(3). Figure 2a indicates that all coefficients of S(1) are positive: this indicates a mode of the magnetospheric system in which all measures of activity in the system vector S increase or decrease in unison, with S(1) representing a “global activity index”. Figure 2b indicates that all of the coefficients of D(1) are positive. The variables in the driver state vector D (Table 1) and their signs were all chosen so that a positive increase in each variable would result in a generally accepted increase in magnetospheric activity. The individual variables on the right-hand side of Eq. (1b) have all been correlatively associated with the driving of magnetospheric activity (Berthelier, 1976; Borovsky and Funsten, 2003; Newell et al., 2007; Borovsky and Denton, 2014; Borovsky and Birn, 2014; Osmane et al., 2015). S(1) is selected by the CCA process to have highest correlation with solar-wind variability: S(1) is focused on activity that reacts to the solar-wind driver.
Using the linear-regression curve in Fig. 1 as a “prediction” of the value of S(1) from knowledge of the value of D(1) yields
In Fig. 3 the autocorrelation functions of S(1)(t) (red curve), D(1)(t) (blue curve), and S(1)(t)−S(1)pred(t) (green curve) are plotted. In Fig. 3a it is seen that the autocorrelation functions of S(1) and D(1) are very similar, with 1∕e autocorrelation times of 23.3 h for S(1) and 22.7 h for D(1). In Fig. 3b the three autocorrelation functions are plotted for time shifts up to 40 d. Note the 27 d peak in the autocorrelation functions of D(1)(t) and S(1)(t): this is associated with the 27 d rotation period of the Sun as viewed from the Earth and the persistence of features on the solar surface that give rise to solar wind with characteristic properties. This causes the driver D(t) properties to have a 27 d periodicity, which drives the system S(t) with a 27 d periodicity.
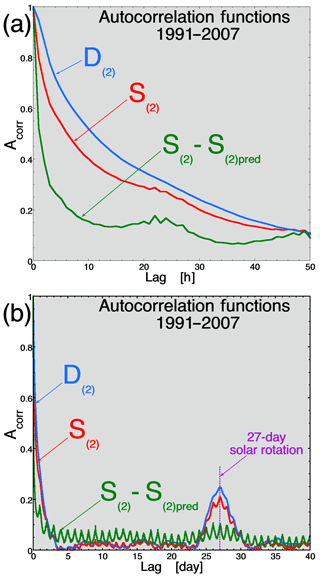
Figure 3The autocorrelation functions for the system scalar S(1) (red), the driver scalar D(1) (blue), and the unaccounted-for variance E(1)E(1)pred (green) are plotted. In panel (a) the plot extends to 50 h and in panel (b) the plot extends to 40 d.
The quantity S(1)−S(1)pred is the portion of S(1)(t) that is not accounted for by D(1)(t), i.e., the unaccounted-for variance of S(1)(t). S(1)(t)−S(1)pred(t) is completely uncorrelated with D(1)(t). Further, S(1)(t)−S(1)pred(t) is completely uncorrelated with each of the eight individual solar-wind variables on the right-hand side of Eq. (1b). Since S(1) is so similar to D(1), the standard analyses of the S(1)(t) time series (e.g., determining the correlation dimension, examining the state space, or Fourier analyzing; Sharma et al., 2005a; Vassiliadis, 2006) would largely be an analysis of the properties of the solar-wind time series D(1)(t) – not so for S(1)(t)−S(1)pred(t), which is uncorrelated with D(1). The autocorrelation function of S(1)(t)−S(1)pred(t) in Fig. 3a is very different from the autocorrelation function of D(1): the 1∕e autocorrelation time of S(1)(t)−S(1)pred(t) is 2.4 h. Determining what the unaccounted-for variance S(1)−S(1)pred originates from is of great interest. Four suggestions of what contributes to S(1)−S(1)pred are made here. First, some fraction of S(1)−S(1)pred may be associated with noise in the various measurements of the magnetospheric system and of the solar wind. Shot noise (random noise in the values of the variables) would have an autocorrelation time of less than 1 h, the autocorrelation function of the shot-noise going from 1 to 0 in one data-resolution time shift (cf. Sect. 2.4 of Borovsky et al., 1997). Second, some fraction of S(1)(t)−S(1)pred(t) may be owed to errors in the measurement values in the state vectors S(t) and D(t). Errors in the values of the variables of D could be caused by the spatial structure of the solar wind and the measuring spacecraft upstream of the Earth not intercepting the exact solar-wind structures that hit and drive the Earth (cf. Weimer et al., 2003; Borovsky, 2018a): this could affect all of the variables of D. Extrapolating local measures to estimate global properties can also lead to errors: this might affect the hemispheric particle-precipitation variables mPe and mPi (Emery et al., 2008) in S and also the magnetospheric pressure values Pips (Borovsky, 2017) in S. Variables reacting to more than one physical process (such as and Pips) could also appear to have error in the values when relating the values to D(1). Third, unaccounted-for time lags between solar-wind variables and magnetospheric variables may be resulting in weakened correlations: most time lags are 1 h or less, but measurements of magnetospheric particle populations can have lags of several hours (e.g., Denton and Borovsky, 2009; Borovsky, 2017). The fourth suggestion is that some fraction of S(1)(t)−S(1)pred(t) might be associated with system variations that are not directly associated with the solar-wind driver as measured by D. The autocorrelation time of S(1)(t)−S(1)pred(t) is approximately the 2–3 h time duration of a magnetospheric substorm (Borovsky et al., 1993; Weimer, 1994; Chu et al., 2015). Substorms are large transients in the reaction of the magnetospheric system to solar-wind driving. (Substorms have been described as self-organized criticality events in the driven magnetospheric system; Klimas et al., 2000.) The occurrence of a substorm is notoriously difficult to predict from solar-wind data (Freeman and Morley, 2004; Hsu and McPherron, 2009; Newell and Liou, 2011). The timing of substorm occurrence would be particularly difficult to infer from the 1 h resolution variables going into D because of the 3 h smoothing used on the clock-angle term in Eq. (1b) for D(1), with the clock angle being critical for substorm occurrence (Newell and Liou, 2011). The occurrence of a substorm would produce signatures in many of the variables used in S(1), typically an enhancement in the variable's amplitude lasting 2–3 h (Weimer, 1994).
To investigate this substorm hypothesis for S(1)(t)−S(1)pred(t), the variables D(1)(t), S(1)(t), and S(1)(t)−S(1)pred(t) are superposed-epoch averaged in Fig. 4 for a collection of 2155 substorm events; the collection is from Borovsky and Yakymenko (2017). The zero epoch in Fig. 4 is the onset time of each of the 2155 substorms. Substorms are associated with intervals of driving of the magnetosphere (e.g., Caan et al., 1977; Morley and Freeman, 2007); this is indicated by the increase in the superposed average of D(1) beginning prior to the onset time in Fig. 4. However, substorms also represent a transient release of stored energy in the magnetosphere (Birn et al., 2006); this is indicated in Fig. 4 by the superposed average of S(1) exceeding the superposed average of D(1) after the substorm onset and by the positive perturbation of the S(1)−S(1)pred curve after onset. The S(1)−S(1)pred curve indicates a transient in S(1) that is unaccounted for by D(1) associated with the occurrence of substorms. The autocorrelation time of the green superposed-average S(1)−S(1)pred time series plotted in Fig. 4 is 2.6 h, similar to the Fig. 1 autocorrelation time of the full 1991–2007 time series of S(1)−S(1)pred.
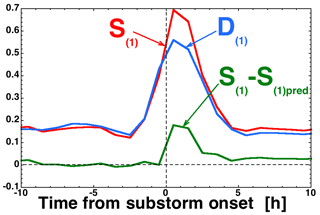
Figure 4Superposed epoch averages of S(1) (red), D(1) (blue), and S(1)−S(1)pred (green) for 2155 substorms. The epoch time (t=0) is the time of onset of each substorm.
Compacting the description of the system from a multidimensional state vector to a few variables S(1), S(2), S(3), … is a form of dimensional reduction to a small set of fundamental latent variables: in that dimensional reduction a potential question is whether the reduced (more-fundamental) variables themselves exhibit a reduction of their embedding dimension from the embedding dimensions of the manifest variables in the state vector. Additionally, it would be valuable to differentiate S(1) from other indices commonly used to characterize magnetospheric activity. In order to achieve this task we use the methodology of Rosso et al. (2007) based on the combined use of permutation entropy (Bandt and Pompe, 2002) and Jensen–Shannon complexity mapping. This mapping developed by Rosso et al. (2007) is particularly useful to disentangle deterministic and stochastic time series. Additionally, one can use the Jensen–Shannon complexity alone to extract correlational structures in time series. In other words, one can seek timescales upon which coherent structures/fluctuations/modes arise. In some instances, coherent modes are signatures of deterministic chaos (Maggs and Morales, 2013) or a reduction to the number of degrees of freedom (Osmane et al., 2019). Readers with little familiarity with these two information theoretic measures can consult the reviews of Riedl et al. (2013) and Zanin et al. (2012) or the pedestrian methodology section found in Osmane et al. (2019). In Figs. 5 and 6, we map the values of AL (red), am (blue), S(1) (black) and D(1) (pink) on the complexity–entropy plane for an interval of 500 h duration with no data gaps, embedding dimensions of d=4, and embedding delay T ranging between 2 and 40 h. Because there are a total of d!=24 ordinal patterns we are limited to embedding delays of the order of 2 d. For embedding delays greater than T=48 h the number of segments becomes too small to ascertain the likelihood of forbidden ordinal patterns. Error bars for the Jensen–Shannon complexity, shown for the zoomed panels of the complexity–entropy planes, are computed as the square root of the number of ordinal patterns divided by the number of segments available. Hence, larger embedded dimensions d, require a larger number of segments to determine whether the Jensen–Shannon complexity lies significantly above the stochastic boundary (see below).
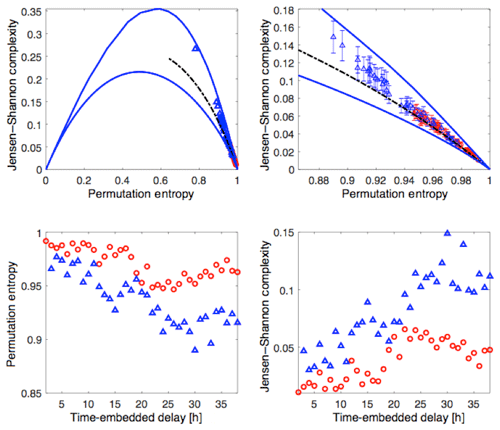
Figure 5Jensen–Shannon complexity and permutation entropy, AL (red) and am (blue) for 500 points with no gaps sampled at 1 h interval, embedding dimension d=4, and embedding delays ranging between 2 and 40 h.
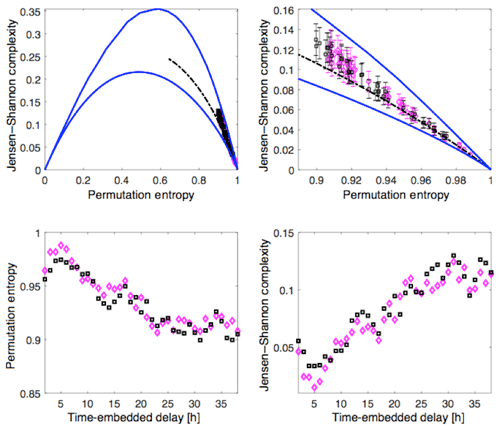
Figure 6Jensen–Shannon complexity and permutation entropy for S(1) (black), D(1) (pink) for 500 points with no gaps sampled at 1 h interval, embedding dimension d=4, and embedding delays ranging between 2 and 40 h.
The bottom left panels in Figs. 5 and 6 show the value of the permutation entropy for AL, am, D(1) and S(1) as a function of embedding delay. Similarly, the bottom right panels show the value of the Jensen–Shannon complexity for AL, am, D(1) and S(1) as a function of embedding delay. What we notice is that all four signals are highly stochastic since the normalized permutation entropy is very close to 1. However, we see that the Jensen–Shannon complexity for S(1) is of comparable magnitude as for am, and it is significantly larger than for AL. This is not a surprise because the construction of S(1) was based on am, and the Jensen–Shannon complexity indicates that the former preserved the correlated structures of the latter on timescales ranging between a few hours to a few days. The top left panel of Figs. 5 and 6 shows the complexity–entropy plane, and the top right panel is a zoom of the right corner where most of the data for AL, am, and S(1) lies. In both figures the blue line curves represent the maximum and minimum value of complexity for a fixed entropy value, and the dashed curve represents the complexity–entropy mapping of fractional Brownian motion (fBm) with Hurst exponent ranging between 0 and 1, which is a stochastic process that also contains correlated structures. The fBm curve is a boundary between deterministic (above) and stochastic (below) fluctuations. We note that AL is effectively stochastic, whereas am and S(1) lie above the fBm boundary for a few tens of hours. The explanation for this behavior from am lies in its construction: it is repeated for 3 h at a time. Hence, ordinal patterns of size d=4 and embedding delays of a few hours will register the repetition as correlated structures. Since S(1) is constructed in part with am, it also contains part of its correlated structure.
For longer embedding delays of the order of seasonal variations ranging from 27 to 45 d (not shown), all four time series overlap and are indistinguishable from stochastic fluctuations. In terms of complexity–entropy plane it translates into a permutation entropy of approximately 1 and a Jensen–Shannon complexity of almost 0. Hence, the system variable S(1), based on various magnetospheric indices, preserves the stochastic and correlational structures of its individual components. The comparable values of the permutation entropy (and therefore Jensen–Shannon complexity) with the system variable with the indices for long times are not fortuitous. The permutation entropy is invariant under any monotonic transformations (for instance, if one scales the time series by a positive real number, or if one takes the logarithm). However, if one used a linear combination of non-monotonic functions, for instance trigonometric functions, then the permutation entropy would not be invariant. Since the Jensen–Shannon complexity is a function of the permutation entropy, it is also invariant under monotonic transformations. Additionally, if one takes an average around the mean of some time series over a time TAU, one will reduce the noise level for fluctuations with timescales less than TAU. Thus, the stochastic nature of the signal will be reduced, and the permutation entropy and Jensen–Shannon complexity would move up in the plane towards the chaotic and/or periodic regions. The equivalence mapping of the information theoretic measures for the system variables and geomagnetic indices is a consequence of the monotonic transformation linking the former to the latter and the absence of coarse-graining of the indices.
3.2 The secondary modes of reaction represented by S(2) and S(3)
In Fig. 7a and b the second and third scalar pairs are plotted, S(2) as a function of D(2) and S(3) as a function of D(3), respectively (Eqs. 2 and 3). The correlation coefficient for the second pair is still quite high (rcorr=0.775) but lower than that of the first pair (Fig. 1). This correlation coefficient rcorr=0.775 for the secondary mode is better than correlations obtained in most studies of solar-wind–magnetosphere coupling using single measures of the magnetospheric system (e.g., Table 3 of Newell et al., 2007; Table 1 of Borovsky, 2013). D(2) describes % of the variance of S(2). In Fig. 7b the correlation coefficient for the third pair is low (rcorr=0.456); D(3) only describes % of the variance of S(3). Canonical pairs beyond the third pair have even weaker correlations.
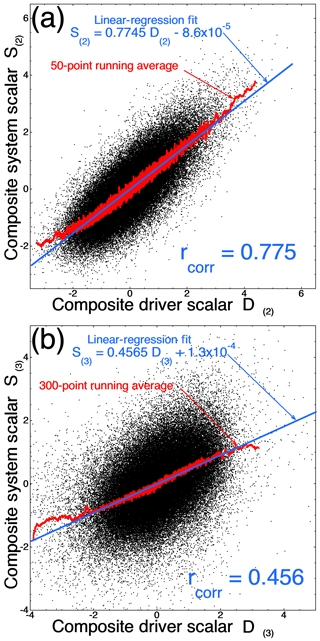
Figure 7For the 1 h resolution 1991–2007 data set, the aggregate system scalar S(2) is plotted as a function of the driver scalar D(2) in panel (a) and the aggregate system scalar S(3) is plotted as a function of the driver scalar D(3) in panel (b). Each black point is 1 h of data.
Figure 2c shows that mode S(2) (Fig. 7a) is dominated by opposite-signed coefficients for mPi and mPe, which respectively are measures of the global ion precipitation into the atmosphere versus the global electron precipitation into the atmosphere. In this S(2) mode the intensity of ion and electron precipitation reacts oppositely. Figure 2d shows that D(2) (the driver of S(2)) is dominated by the solar wind number density nsw opposite to the clock angle sin 2(θclock∕2) of the solar-wind magnetic field, with the solar wind density increasing while the clock angle decreases resulting in more ion precipitation and less electron precipitation. This ion-versus-electron precipitation mode is a newly uncovered mode of reaction of the magnetosphere–ionosphere–thermosphere system to the solar wind.
Figure 2e shows that S(3) (Fig. 7b) is characterized by the polar cap index (PCI) and mPi acting oppositely to Kp and am. PCI is a measure of high-latitude electrical currents in the magnetosphere, and mPi is a measure of high-latitude ion precipitation; Kp and am are measures of global magnetospheric convection. This S(3) mode is very similar to a high-latitude versus convection mode uncovered by Borovsky (2014) and by Holappa et al. (2014). Figure 2f indicates that the driver D(3) for this mode is the solar wind velocity acting oppositely to the magnetic field clock angle: the wind velocity increasing while the clock angle is reduced producing more convection and less high-latitude activity, or the wind slowing down while the clock angle increases producing less convection and more high-latitude activity.
The aggregate variable S(1) acts as a global activity index for the magnetospheric system: S(1) is new and unfamiliar, and experience using S(1) is needed to gain an understanding of the full usefulness of this measure. S(1) could be thought of as a next-generation magnetospheric index. In Earth systems science global aggregate variables are familiar: the global warming index (Hasselman, 1997; Haustein et al., 2016), the global mean sea level (Vermeer and Rahmstorf, 2009), the mean global temperature (Hansen et al., 2006), the Palmer Drought Severity Index (Wells et al., 2004), and Sea Surface Temperature indices (Kaplan et al., 1998). And stock-market aggregate indices are well known and are more-meaningful gauges of an economy than the price of a single stock (e.g., Pan and Mishra, 2018). Here the aggregate variable S(1) is mathematically derived. The individual variables of S that go into the definition of S(1) represent familiar and identifiable aspects of activity in the magnetospheric system. The composite variable S(1) is a mix of these understood measurements, the mix reflecting some global properties of the system's reaction to the solar wind. Unfamiliar as it is, the composite-scalar D(1)→S(1) reduction of the state-vector D→S picture exhibits some outright advantages for the magnetospheric system. This is particularly true in comparison with the standard method of analysis of magnetospheric driving by the solar wind that uses only a single measurement of magnetospheric activity and a single function of solar-wind variables. Four advantages are discussed in the following four paragraphs.
-
Linearity. The plotted points in Fig. 1 indicate that there is a linear response of the composite system variable S(1)(t) to the composite driver D(1)(t). Usually, single measures of the magnetosphere tend to have a nonlinear response to the solar wind (e.g., Voros, 1994; Valdivia et al., 1996; Sharma et al., 2005b; Borovsky, 2013; Stepanova and Valdivia, 2016), with the individual activity variables saturating (becoming anomalously weak) when solar-wind driving becomes strong (e.g., Fig. 3 of Reiff and Luhmann, 1986; Fig. 17 of Lavraud and Borovsky, 2008; Fig. 6 of Borovsky, 2013). Such a saturation is not seen for S(1) driven by D(1). Undoubtedly, the linearity of the result is in part owed to the maximizing of the “linear” correlation coefficient in the CCA process. The linearity of the S(1)-vs.-D(1) relation has a great advantage: the same mathematical relationship between S(1) and D(1) (i.e., Eq. 4) holds for weak driving of the system (small D(1)) (e.g., Kerns and Gussenhoven, 1990) and for strong driving of the system (large D(1)) (e.g., Sharma and Veeramani, 2011).
-
Low noise. The high correlation between S(1) and D(1) (cf. Fig. 1) indicates that there is a relatively low level of noise in the linear-regression fit to S(1): the activity in the system as described by S(1) responds directly to the solar-wind driving as described by D(1). For example, the unaccounted-for variance of S(1) is only 15.2 %. Single measures of the magnetospheric system have much weaker Pearson linear correlation coefficients with solar-wind variables than S(1) and D(1) do. Examples can be found in Table 3 of Newell et al. (2007) and Table 1 of Borovsky (2013): the maximum correlation coefficient in those tables is 0.860 (for the Dst index), but usually it is much lower. The lower noise is also confirmed by the Jensen–Shannon complexity analysis of S(1): the points for S(1) and D(1) sit closer to the maximum complexity curve than AL and other indices. The lower noise (and higher rcorr) reduces “regression dilution bias” (Bock and Petersen, 1975; Hutcheon et al., 2010) when the system activity is fit by the driver strength. Regression dilution bias can lead to spurious interpretation of trends in the data when subsets of the data are compared, particularly when a subset with systematically weaker driving is compared with a subset with systematically stronger driving.
-
High prediction efficiency. In magnetospheric physics, predicting what the reaction of the magnetospheric system will be to measured upstream solar-wind conditions is very important: i.e., the prediction of “space weather” (Singer et al., 2001). The high correlation between S(1) and D(1) means that there will be a high prediction efficiency when the value of S(1) is predicted from knowledge of the value of D(1). Note that this is a high prediction of S(1)(t) without using past values of S(1), just using the present value of D(1)(t). By optimizing the Pearson linear correlation coefficient between S and D, S(1) was designed to focus on aspects of the magnetospheric system that are responsive to the conditions of the solar wind. Internal dynamics of the system that are not dependent on the time-varying state of the driver are de-emphasized in S(1).
-
Compactness of the description. Reductionist analysis has concluded that the magnetosphere–ionosphere–thermosphere system is extremely complex (e.g., Siscoe, 2011; Eastwood et al., 2015; Borovsky and Valdivia, 2018). As it is driven by the solar wind, there are major outstanding issues as to how the system functions (e.g., Denton et al., 2016). Having a single scalar variable S(1)(t) that describes a universal global reaction of the system to its driver promises to yield insight as to how the combined system operates.
-
Uncovering new modes of reaction. In the CCA analysis of the system and driver state vectors, two additional aggregate variables S(2)(t) and S(3)(t) were generated (Eqs. 2a and 3a). Analysis in Sect. 3.2 showed these two variables to represent two modes of reaction of the system to the driver that are independent of (uncorrelated with) the global-activity mode represented by S(1)(t). The mode represented by S(3) is known (having been independently discovered by this CCA methodology in Borovsky, 2014, and by a principle-components methodology in Holappa et al., 2014), but the mode represented by S(2) has until now been unknown. The CCA methodology used here also identifies the aggregate driver variable that drives each of the independent modes. In the future, expanding the system state vector to include a larger number of measurements in the diverse magnetospheric system should enable this state-vector-reduction methodology to uncover more unknown modes of reaction of the system to the driver. Once a reaction and its driver are uncovered, reductionist analysis can be applied to determine the physical reasons why the mode arises.
For a system measured by multiple time-dependent variables (which are collected into a time-dependent system state vector S(t)), with that system driven by multiple time-dependent factors (inputs) (which are collected into a time-dependent driver state vector D(t)), canonical correlation analysis (CCA) can be used to reduce the D(t)→S(t) state-vector picture to a D(i)(t)→S(i)(t) composite-scalar picture. The reduction will work, even if there is influence on the driver by the system (i.e., D(t)↔S(t)). The advantageous properties of this reduction that were examined for the magnetospheric system should apply to systems in general.
Future developments of this methodology will focus on the introduction of time lags between the driver and the system, on the introduction of integro-differential correlations rather than algebraic correlations (e.g., Borovsky, 2017), and on the use of dynamic canonical correlation analysis (e.g., Dong and Qin, 2018a, b).
The 1991–2007 data set of hourly values of S(1), S(2), S(3), D(1), D(2), and D(3) has been made available at https://doi.org/10.5281/zenodo.1560686 (Borovsky, 2018b) and at https://doi.org/10.17605/OSF.IO/QYTNJ (Borovsky, 2018c) as a tab-delimited text file.
The time-dependent variables of the magnetospheric system state vector and the solar-wind driver state vector are listed in Table 1.
The magnetospheric variables measure various aspects of activity in the magnetosphere. The auroral upper index AU (Davis and Sugiura, 1966) measures the electrical current in the high-latitude ionosphere: this variable is taken to be a measure of electrical currents in the dayside magnetosphere (Goertz et al., 1993). The auroral lower index AL (Davis and Sugiura, 1966) measures the electrical current in the high-latitude nightside ionosphere: this variable is taken to be a measure of auroral activity in the nightside magnetosphere (Goertz et al., 1993). The polar cap index PCI is a measure of the strength of cross-polar-cap electrical current in the ionosphere (Troshichev et al., 1988). The planetary K index Kp is a measure of the strength of global convection in the magnetosphere (Thomsen, 2004). The range index am (Mayaud, 1980) is another measure of the strength of global magnetospheric convection. The disturbance storm-time index Dst measures plasma pressure in the inner magnetosphere (Dessler and Parker, 1959); Dst also reacts to the currents on the dayside boundary of the magnetosphere and to the cross-magnetotail currents in the nightside magnetosphere. The time derivative of the magnitude of the Dst index is a compound measure of magnetospheric activity: when is positive, hot plasma is being convected from the magnetotail into the dipolar portion of the magnetosphere, and when is negative, convection has recently subsided. The variables mPe and mPi are estimates of the full-Earth power in magnetospheric electron precipitation into the atmosphere and magnetospheric ion precipitation into the atmosphere (Emery et al., 2008, 2009), with these estimates coming from observations on only a few spacecraft in orbit around the Earth. The average of the ion-plasma-sheet particle pressure Pips around the Earth (Borovsky, 2017) is obtained from three to five spacecraft.
The variables going into the solar-wind driver state vector are various measures of the time-dependent solar wind at Earth. The solar wind speed vsw ranges from 244 to 1045 km s−1 in the 1991–2007 data set. The solar wind number density ranges from 0.3 to 98.2 particles cm−3 in the data set. Bz is the magnetic-field component in the solar-wind plasma that is approximately aligned with the Earth's magnetic-dipole orientation. The function f(M) (Borovsky and Birn, 2014) is a function of the solar-wind Mach number M that accounts for the properties of the bow shock that forms upstream of the Earth in the supersonic solar-wind flow. The clock angle θclock measures the angular alignment of the solar-wind magnetic-field vector with the Earth's magnetic-dipole orientation. The angle θBn measures the orientation of the solar-wind magnetic-field vector with respect to the Sun–Earth line. F10.7 is the 10.7 cm radio flux from the Sun, a proxy for the ionization of the upper atmosphere of the Earth by solar photons.
JEB devised this study and performed the CCA analysis. AO performed the complexity and entropy analysis. Both authors are responsible for the interpretation of the results and for the writing of the manuscript.
The authors declare that they have no conflict of interest.
The authors thank Mick Denton and Juan Alejandro Valdivia for helpful discussions.
This work was supported by the NSF GEM Program via award AGS-1502947, by the NASA Heliophysics LWS TRT program via grants NNX16AB75G and NNX14AN90G, by the NSF Solar-Terrestrial Program via grant AGS-12GG13659, by the NASA Heliophysics Guest Investigator Program via grant NNX17AB71G, by the NSF SHINE program via award AGS-1723416, and by the Academy of Finland via grant no. 297688/2015.
This paper was edited by A. Surjalal Sharma and reviewed by Marina Stepanova and one anonymous referee.
Bandt, C. and Pompe, B.: Permutation Entropy: A Natural Complexity measure for time series, Phys. Rev. Lett., 88, 174102, https://doi.org/10.1103/PhysRevLett.88.174102, 2002.
Berthelier, A.: Influence of the polarity of the interplanetary magnetic field on the annual and the diurnal variations of magnetic activity, J. Geophys. Res., 81, 4546–4552, 1976.
Birn, J., Hesse, M., and Schindler, K.: Modeling of the magnetospheric response to the dynamic solar wind, Space Sci. Rev., 124, 103–116, 2006.
Bock, R. D. and Petersen, A C.: A multivariate correction for attenuation, Biometrika 62, 673–678, 1975.
Borovsky, J. E.: Physics based solar-wind driver functions for the magnetosphere: Combining the reconnection-coupled MHD generator with the viscous interaction, J. Geophys. Res., 118, 7119–7150, 2013.
Borovsky, J. E.: Canonical correlation analysis of the combined solar-wind and geomagnetic-index data sets, J. Geophys. Res., 119, 5364–5381, 2014.
Borovsky, J. E.: Time-integral correlations of multiple variables with the relativistic-electron flux at geosynchronous orbit: The strong roles of the substorm-injected electrons and the ion plasma sheet, J. Geophys. Res., 122, 11961–11990, 2017.
Borovsky, J. E.: The spatial structure of the oncoming solar wind at Earth, J. Atmos. Sol.-Terr. Phys., 177, 2–11, https://doi.org/10.1016/j.jastp.2017.03.014 , 2018a.
Borovsky, J. E.: Aggregate variables for International Journal of General Systems, data set, https://doi.org/10.5281/zenodo.1560686, 2018b.
Borovsky, J. E.: Hourly data 1991–2007 of three aggregate variables describing the magnetospheric system and three aggregate solar-wind driver variables, data set, https://doi.org/10.17605/OSF.IO/QYTNJ, 2018c.
Borovsky, J. E. and Birn, J.: The solar-wind electric field does not control the dayside reconnection rate, J. Geophys. Res., 119, 751–760, 2014.
Borovsky, J. E. and Denton, M. H.: Exploring the cross-correlations and autocorrelations of the ULF indices and incorporating the ULF indices into the systems science of the solar-wind-driven magnetosphere, J. Geophys. Res., 119, 4307–4334, 2014.
Borovsky, J. E. and Denton, M. H.: Exploration of a composite index to describe magnetospheric activity: Reduction of the magnetospheric state vector to a single scalar, J. Geophys. Res., 123, 7384–7412, 2018.
Borovsky, J. E. and Funsten, H. O.: Role of Solar Wind Turbulence in the Coupling of the Solar Wind to the Earth's Magnetosphere, J. Geophys. Res., 108, 1246, https://doi.org/10.1029/2002JA009601 , 2003.
Borovsky, J. E. and Valdivia, J. A.: The Earth's magnetosphere: A systems science overview and assessment, Surv. Geophys., 39, 817–859, https://doi.org/10.1007/s10712-018-9487-x, 2018.
Borovsky, J. E. and Yakymenko, K.: Systems science of the magnetosphere: Creating indices of substorm activity, of the substorm-injected electron population, and of the electron radiation belt, J. Geophys. Res., 122, 10012–10035, 2017.
Borovsky, J. E., Nemzek, R. J., and Belian, R. D.: The Occurrence Rate of Magnetospheric-Substorm Onsets: Random and Periodic Substorms, J. Geophys. Res., 98, 3807–3813, 1993.
Borovsky, J. E., Elphic, R. C., Funsten, H. O., and Thomsen, M. F.: The Earth's Plasma Sheet as a Laboratory for Turbulence in High-Beta MHD, J. Plasma Phys., 57, 1–34, 1997.
Caan, M. N., McPherron, R. L., and Russell, C. T.: Characteristics of the association between interplanetary magnetic field and substorms, J. Geophys. Res., 82, 4837–4842, 1977.
Chapman, S. C., Dendy, R. O., and Watkins, N. W.: Robustness and scaling: key observables in the complex dynamic magnetosphere, Plasma Phys. Control. Fusion, 46, B157–B166, 2004.
Chu, X., McPherron, R. L., Hsu,T.-S., and Angelopoulos, V.: Solar cycle dependence of substorm occurrence and duration: Implications for onset, J. Geophys. Res., 120, 2808–2818, 2015.
Clauer, C. R., McPherron, R. L., Searls, C., and Kivelson, M. G.: Solar wind control of auroral zone geomagnetic activity, Geophys. Res. Lett., 8, 915–918, 1981.
Davis, T. N. and Sugiura, M.: Auroral electrojet activity index AE and its Universal Time variations, J. Geophys. Res., 71, 785–801, 1966.
Denton, M. H. and Borovsky, J. E.: The superdense plasma sheet in the magnetosphere during high-speed-steam-driven storms: Plasma transport timescales, J. Atmos. Sol.-Terr. Phys., 71, 1045–1058, 2009.
Denton, M. H., Borovsky, J. E., Stepanova, M., and Valdivia, J. A.: Unsolved Problems of Magnetospheric Physics, J. Geophys. Res., 121, 10783–10785, 2016.
Dessler, A. J. and Parker, E. N.: Hydromagnetic theory of geomagnetic storms, J. Geophys. Res., 64, 2239–2252, 1959.
Dong, Y. and Qin, S. J.: Dynamic-inner canonical correlation and causality analysis for high dimensional time series data, Inter. Feder. Automatic Contr. Papers, 51, 476–481, 2018a.
Dong, Y. and Qin, S. J.: Dynamic latent variable analysis for process operations and control, Comput. Chemical Engin., 114, 69–80, 2018b.
Eastwood, J. P., Hietala, H., Toth, G., Phan, T. D., and Fujimoto, M.: What controls the structure and dynamics of the Earth's magnetosphere?, Space Sci. Rev., 188, 251–286, 2015.
Emery B. A., Coumans, V., Evans, D. S., Germany, G. A., Greer, M. S., Holeman, E., Kadinsky-Cade, K., Rich, F. J., and Xu, W.: Seasonal, Kp, solar wind, and solar flux variations in long-term single-pass satellite estimates of electron and ion auroral hemispheric power, J. Geophys. Res., 113, A06311, https://doi.org/10.1029/2007JA012866, 2008.
Emery, B. A., Richardson, I. G., Evans, D. S., and Rich, F. J.: Solar wind structure sources and periodicities of auroral electron power over three solar cycles, J. Atmos. Sol.-Terr. Phys., 71, 1157–1175, 2009.
Freeman, M. P. and Morley, S. K.: A minimal substorm model that explains the observed statistical distribution of times between substorms, Geophys. Res. Lett., 31, L12807, https://doi.org/10.1029/2004GL019989, 2004.
Goertz, C. K., Shan, L.-H., and Smith, R. A.: Prediction of geomagnetic activity, J. Geophys. Res., 98, 7673–7684, 1993.
Hair, J. F., Black, W. C., Babin, B. J., and Anderson, R. E.: Canonical Correlation: A Supplement to Multivariate Data Analysis, Pearson Prentice Hall Publishing, Upper Saddle River, New Jersey, 2010.
Hansen, J., Sato, M., Ruedy, R., Lo, K., Lea, D. W., and Medina-Elizade, M.: Global temperature change, P. Natl. Acad. Sci. USA, 103, 14288–14293, 2006.
Hasselmann, K.: Multi-pattern fingerprint method for detection and attiribution of climate change, Clim. Dynam., 13, 601–611, 1997.
Haustein, K., Allen, M. R., Forste, P. M., Otto, F. E. L., Mitchell, D. M., Matthews, H. D., and Frame, D. J.: A real-time Global Warming Index, Sci. Rep., 7, 15417, https://doi.org/10.1038/s41598-017-14828-5, 2016.
Holappa, L., Mursula, K., Asikainen, T., and Richardson, I. G.: Annual fractions of high-speed streams from principal component analysis of local geomagnetic activity, J. Geophys. Res., 119, 4544, https://doi.org/10.1002/2014JA019958, 2014.
Holzer, R. E. and Slavin, J. A.: A correlative study of magnetic flux transfer in the magnetosphere, J. Geophys. Res., 84, 2573–2578, 1979.
Horton, W., Smith, J. P., Weigel, R., Crabtree, C., Doxas, I., Goode, B., and Cary, J.: The solar-wind driven magnetosphere-ionosphere as a complex dynamical system, Phys. Plasmas, 6, 4178–4184, 1999.
Hsu, T.-S. and McPherron, R. L.: A statistical study of the spatial structure of interplanetary magnetic field substorm triggers and their associated magnetic response, J. Geophys. Res., 114, A02223, https://doi.org/10.1029/2008JA013439, 2009.
Hutcheon, J. A., Chiolero, A., and Hanley, J. A.: Random measurement error and regression dilution bias, BMJ, 340, 1402–1406, 2010.
Johnson, R. A. and Wichern, D. W.: Applied Multivariate Statistical Analysis, 6th edn., Pearson Prentice Hall, Upper Saddle River, New Jersey, 2007.
Kaplan, A., Cane, M. A., Kushnir, Y., Clement, A. C., Blumenthal, M. B., and Rajagoplalan, B.: Analyses of global sea surface temperature 1956–1991, J. Geophys. Res., 103, 18567–18589, 1998.
Kerns, K. J. and Gussenhoven, M. S.: Solar wind conditions for a quiet magnetosphere, J. Geophys. Res., 95, 20867–20875, 1990.
King, J. H. and Papitashvili, N. E.: Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data, J. Geophys. Res., 110, 2104, https://doi.org/10.1029/2004JA010649, 2005.
Klimas, A. J., Valdivia, J. A., Vassiliadis, D., Baker, D. N., Hesse, M., and Takalo, J.: Self-organized criticality in the substorm phenomenon and its relation to localized reconnection in the magnetospheric plasma sheet, J. Geophys. Res., 105, 18765–18780, 2000.
Lavraud, B. and Borovsky, J. E.: Altered solar wind-magnetosphere interaction at low Mach numbers: Coronal mass ejections, J. Geophys. Res., 113, A00B08, https://doi.org/10.1029/2008JA013192, 2008.
Lyon, J. G.: The solar wind-magnetosphere-ionosphere system, Science, 288, 1987–1991, 2000.
Maggs, J. E. and Morales, G. J.: Permutation entropy analysis of temperature fluctuations from a basic electron heat transport experiment, Plasma Phys. Control. Fusion, 55, 8, https://doi.org/10.1088/0741-3335/55/8/085015, 2013.
Mayaud, P. N.: Derivation, Meaning, and Use of Geomagnetic Indices, Sect. 5.2, American Geophysical Union, Washington, DC, 1980.
Morley, S. K. and Freeman, M. P.: On the association between northward turnings of the interplanetary magnetic field and substorm onsets, Geophys. Res. Lett., 34, L08104, https://doi.org/10.1029/2006GL028891, 2007.
Newell, P. T. and Liou, K.: Solar wind driving and substorm triggering, J. Geophys. Res., 116, A03229, https://doi.org/10.1029/2010JA016139, 2011.
Newell, P. T., Sotirelis, T., Liou,, K. Meng, C. I., and Rich, F. J.: A nearly universal solar wind-magnetosphere coupling function inferred from 10 magnetospheric state variables, J. Geophys. Res., 112, A01206, https://doi.org/10.1029/2006JA012015, 2007.
Nimon, K., Henson, R. K., and Gates, M. S.: Revisiting interpretation of canonical correlation analysis: A tutorial and demonstration of canonical commonality analysis, Multivariate Behav. Res., 45, 702–724, 2010.
Osmane, A., Dimmock, A. P., Naderpour. R., Pulkkinen, T. I., and Nykyri, K.: The impact of solar wind ULF Bz fluctuations on geomagnetic activity for viscous timescales during strongly northward and southward IMF, J. Geophys. Res., 120, 9307–9322, 2015.
Osmane, A., Dimmock, A. P., and Pulkkinen, T. I.: Jensen-Shannon complexity and permutation entropy analysis of geomagnetic auroral currents, J. Geophys. Res., 124, 2541–2551, 2019.
Otto, A.: The magnetosphere, Lecture Notes Phys., 656, 133–192, 2005.
Pan, L. and Mishra, V.: Stock market development and economic growth: Empirical evidence from China, Eco. Modell., 68, 661–673, 2018.
Reiff, P. H. and Luhmann, J. G.: Solar wind control of the polar-cap voltage, in: Solar Wind-Magnetosphere Coupling, edited by: Kamide, Y. and Slavin, J. A., Kluwer Academic Publishers, Norwell, Massachusetts, 453–476, 1986.
Riedl, M., Muller, A., and Wessel, N.: Practical considerations of permutation entropy, Euro. Phys. J. Spec. Top., 222, 249–262, https://doi.org/10.1140/epjst/e2013-01862-7, 2013.
Rosso, O. A., Larrondo, H. A., Martin, M. T., Plastino, A., and Fuentes, M. A.: Distinguishing Noise from Chaos, Phys. Rev. Lett., 99, 154102, https://doi.org/10.1103/PhysRevLett.99.154102, 2007.
Sharma, A. S.: The magnetosphere: A complex driven system, AIP Conf. Proc., 1308, 120–131, 2010.
Sharma, A. S. and Veeramani, T.: Extreme events and long-range correlations in space weather, Nonlin. Processes Geophys., 18, 719–725, https://doi.org/10.5194/npg-18-719-2011, 2011.
Sharma, A. S., Ukhorskiy, A. Y., and Sitno, M. I.: Global and multiscale phenomena of the magnetosphere, in: Nonlinear Phenomena in Plasmas, edited by: Sharma, A. S. and Kaw, P. K., Springer, Heidelberg, Germany, 117–144, 2005a.
Sharma, A. S., Baker, D. N., and Borovsky, J. E.: Nonequilibrium phenomena in the magnetosphere: Phase transition, self-organized criticality, and turbulence, in: Nonequilibrium Phenomena Plasmas, edited by: Sharma, A. S. and Kaw, P. K., Springer, Heidelberg, Germany, 3–22, 2005b.
Singer, H. J., Heckman, G. R., and Hirman, J. W.: Space weather forecasting: A grand challenge, Geophys. Monog. Ser., 125, 23–29, 2001.
Siscoe, G. L.: Aspects of global coherence of magnetospheric behaviour, J. Atmos. Sol.-Terr. Phys., 73, 402–419, 2011.
Smith, J. P., Thomsen, M. F., Borovsky, J. E., and Collier, M.: Solar wind density as a driver for the ring current in mild storms, Geophys. Res. Lett., 26, 1797–1800, 1999.
Stepanova, M. and Valdivia. J. A.: Contribution of Latin-American scientists to the study of the magnetosphere of Earth, A review, Adv., Space Res., 58, 1968–1985, 2016.
Stern, D. P.: A brief history of magnetospheric physics before the spaceflight era, Rev. Geophys., 27, 103–114, 1989.
Stern, D. P.: A brief history of magnetospheric physics during the space age, Rev. Geophys., 34, 1–31, 1996.
Thomsen, M. F.: Why Kp is such a good measure of magnetospheric convection, Space Weather, 2, S11044, https://doi.org/10.1029/2004SW000089, 2004.
Troshichev, O. A., Andrezen, V. G., Vennerstrøm, S., and Friis-Christensen, E.: Magnetic activity in the polar cap – A new index, Planet. Space Sci., 11, 1095–1102, 1998.
Valdivia, J. A., Sharma, A. S., and Papadopoulos, K.: Prediction of magnetic storms by nonlinear models, Geophys. Res. Lett., 23, 2899–2902, 1996.
Valdivia, J. A., Rogan, J., Munoz, V., Gomberoff, L., Klimas, A., Vassiliadis, D., Uritsky, V., Sharma, S., Toledo, B., and Wastavino, L.: The magnetosphere as a complex system, Adv. Space Res., 35, 961–971, 2005.
Valdivia, J. A., Rogan, J., Munoz, V., Toledo, B. A., and Stepanova, M.: The magnetosphere as a complex system, Adv. Space Res., 51, 1934–1941, 2013.
Vassiliadis, D.: Systems theory for geospace plasma dynamics, Rev. Geophys., 44, RG2002, https://doi.org/10.1029/2004RG000161, 2006.
Vermeer, M. and Rahmstorf. S.: Global sea level linked to global temperature, P. Natl. Acad. Sci. USA, 106, 21527–21532, 2009.
Voros, Z.: The magnetosphere as a nonlinear system, Stud. Geophys. Geod., 38, 168–186, 1994.
Weimer, D. R.: Substorm time constants, J. Geophys. Res., 99, 11005–11015, 1994.
Weimer, D. R., Ober, D. N., Maynard, N. C., Collier, M. R., McComas, D. J., Ness, N. F., Smith, C. W., and Watermann, J.: Predicting interplanetary magnetic field (IMF) propagation delay times using the minimum variance technique, J. Geophys. Res., 108, 1026, https://doi.org/10.1029/2002JA009405, 2003.
Wells, N., Goddard, W., and Hayes, M. J.: A self-calibrating Palmer Drought Severity Index, J. Climate, 17, 2235–2351, 2004.
Zanin, M., Zunino, L., Rosso, O. A., and Papo, D.: Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review, Entropy, 14, 1553–1577, 2012.
- Abstract
- Introduction
- Creation of composite (aggregate) variables from the state vectors
- Properties of the scalar reduced picture for the magnetospheric system
- Advantages of the reduced (aggregate-variable) representation of the system
- Data availability
- Appendix A: The variables comprising the magnetospheric system state vector and the solar-wind driver state vector
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Creation of composite (aggregate) variables from the state vectors
- Properties of the scalar reduced picture for the magnetospheric system
- Advantages of the reduced (aggregate-variable) representation of the system
- Data availability
- Appendix A: The variables comprising the magnetospheric system state vector and the solar-wind driver state vector
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References





